
The probability distribution of a random variable 'X', taking values 1, 2, 3, 4, 5 is given :
(a) Find the value of p.
(b) Find the mean of X.
( c ) Find the variance of X.
The correct Answer is:(a) 116 (b) 3116 ( c ) 367256.
Step by step video, text & image solution for The probability distribution of a random variable 'X', taking values 1, 2, 3, 4, 5 is given : (a) Find the value of p. (b) Find the mean of X. ( c ) Find the variance of X. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:EXERCISE 13 (f) (LATQ II)
Explore 5 Videos
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:EXERCISE 13 (g) (SATQ)
Explore 2 Videos
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:EXERCISE 13 (f) (SATQ)
Explore 2 Videos
- MATRICESBook:MODERN PUBLICATIONChapter:MATRICESExercise:CHAPTER TEST (3)
Explore 12 Videos
- RELATIONS AND FUNCTIONSBook:MODERN PUBLICATIONChapter:RELATIONS AND FUNCTIONSExercise:CHAPTER TEST (1)
Explore 12 Videos
Similar Questions
Knowledge Check
The probability distribution of a discrete random variable X is given below

The value of k isA8B16C32D48The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
The probability distribution of a random variable X is given by

Then 12σ=
View SolutionThe probability distribution of a random variable is as follows: The variance of x is
View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to

View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probablity distribution of a random variable X ,
the number of defects per 10 meters of a fabric is given by
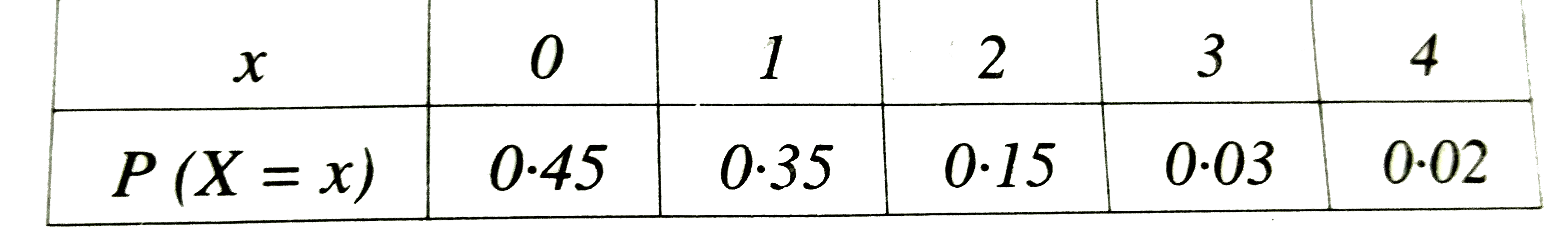
Find the variance of X .
View Solution



