A parallelogram containing a $60^{0}$ angle has perimeter $p$ and its longer diagonal is of length $..$ Find its area.

Video Solution

Text Solution

Verified by Experts

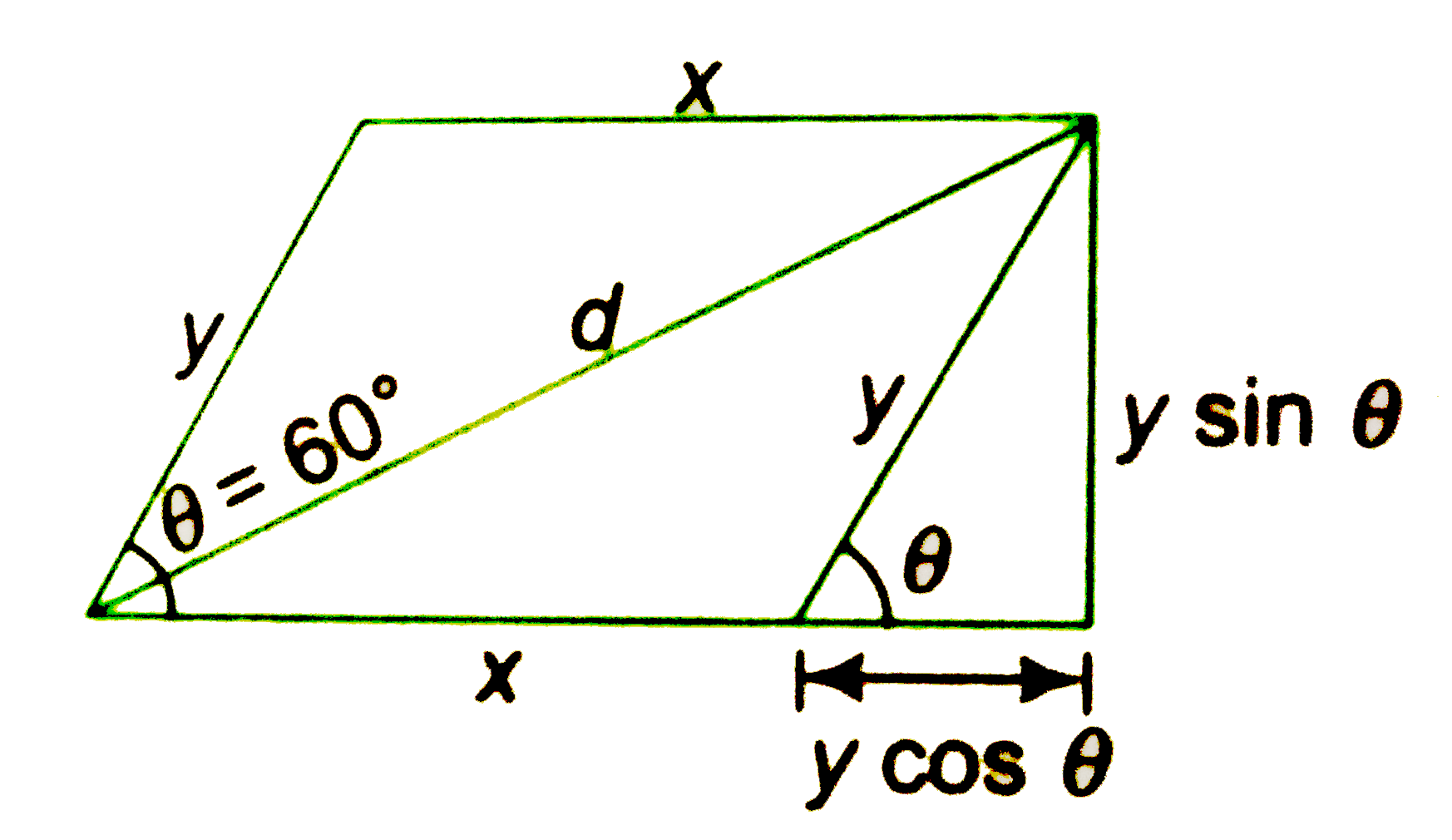
Perimeter,
$2 (x + y) = p$
or $x + y = \frac{p}{2}$
Also, $d^{2} = {(x + y cos θ)}^{2} + y^{2} {sin}^{2} θ \dots (i)$
$= x^{2} + y^{2} + 2 x y cos θ$
$= x^{2} + y^{2} + x y (θ = 60^{\circ})$
$= {(x + y)}^{2} - x y$
$= \frac{p^{2}}{4} - x y$ [using (i)]
or $x y = \frac{p^{2}}{4} - d^{2}$
Now,
Area of parallelogram $= x y {sin 60}^{\circ}$
$= (\frac{p^{2}}{4} - d^{2}) \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{8} (p^{2} - 4 d^{2})$

Updated on:21/07/2023

A rhombus has diagonals of length 8 cm and 6 cm. Find its perimeter.
A24 cm
B28 cm
C18 cm
D20 cm
A rectangle with perimeter 32 cm has greatest area if its length is
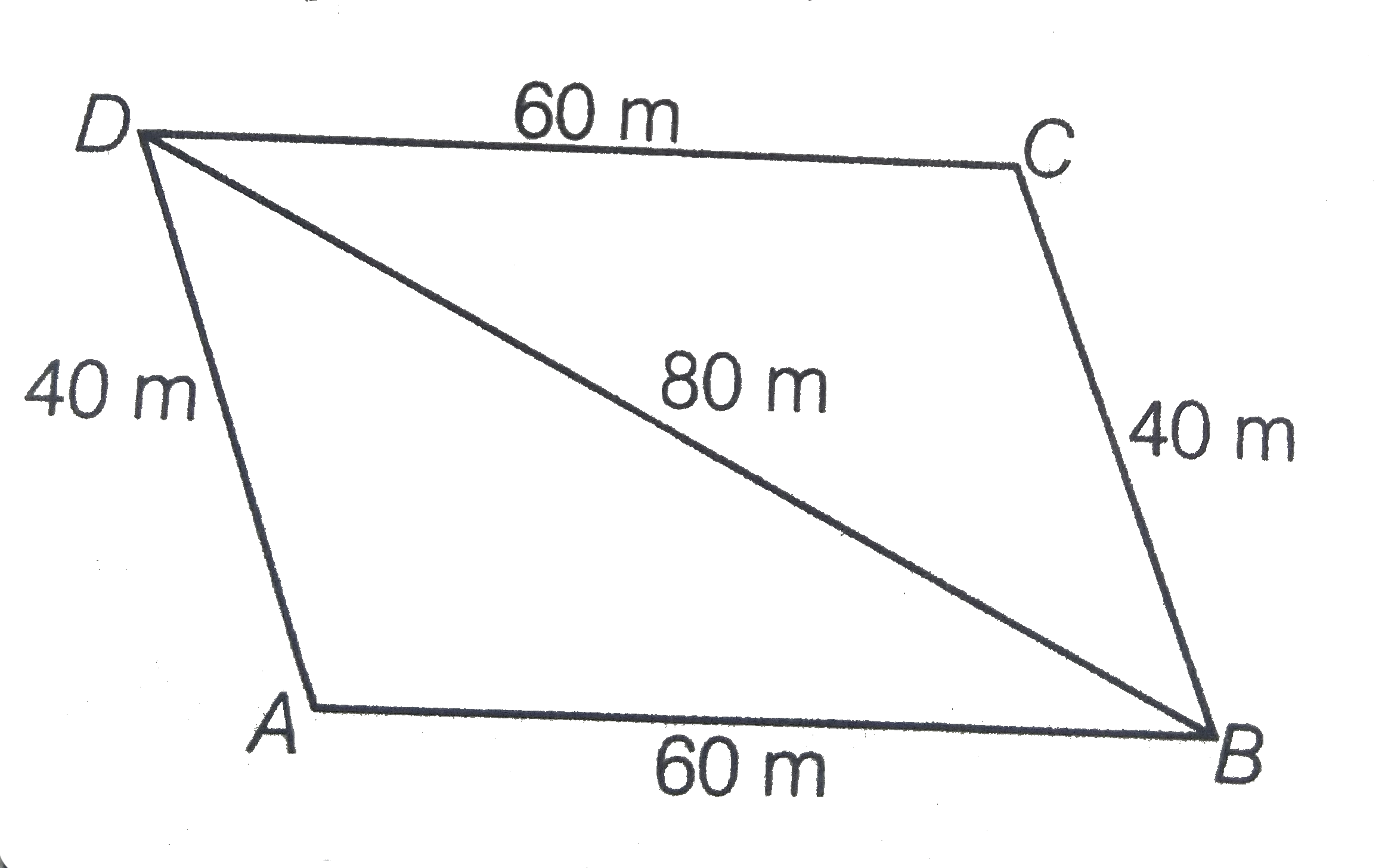
A12
B10
C8
D14
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.

A480 sq. m
B320 sq. m
C $600 \sqrt{15} s q . m$
D $450 \sqrt{15}$ sq . M