Two coherent sources are at distances x1=0.2m and x2=0.08m from a point. Consider the intensity of resultant wave at that point if the frequency of each wave is f=400Hz and velocity of wave in the medium is V=192m/s
The intensity of each wave is I0=60W/m2
To solve the problem, we need to find the resultant intensity of the waves from two coherent sources at given distances from a point. Here’s a step-by-step solution:
Step 1: Calculate the Path Difference
The path difference (Δx) between the two waves is given by the difference in distances from the sources to the point.
Δx=x1−x2=0.2m−0.08m=0.12m
Step 2: Calculate the Wavelength (λ)
Using the relationship between wave velocity (V), frequency (f), and wavelength (λ):
V=fλ⟹λ=Vf
Substituting the given values:
λ=192m/s400Hz=0.48m
Step 3: Calculate the Phase Difference (Δφ)
The phase difference (Δφ) can be calculated using the path difference and wavelength:
Δϕ=2πλΔx
Substituting the values:
Δϕ=2π0.48×0.12
Calculating this gives:
Δϕ=2π×0.120.48=2π4=π2
Step 4: Calculate the Resultant Intensity (I)
The resultant intensity (I) of two coherent waves can be calculated using the formula:
I=I1+I2+2√I1I2cos(Δϕ)
Given that the intensity of each wave I1=I2=I0=60W/m2:
I=I0+I0+2√I0I0cos(π2)
Since cos(π2)=0:
I=60+60+0=120W/m2
Final Answer
The resultant intensity at the point is:
120W/m2
---
The path difference (Δx) between the two waves is given by the difference in distances from the sources to the point.
Using the relationship between wave velocity (V), frequency (f), and wavelength (λ):
The phase difference (Δφ) can be calculated using the path difference and wavelength:
The resultant intensity (I) of two coherent waves can be calculated using the formula:
The resultant intensity at the point is:
Topper's Solved these Questions
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-1
12 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-2
9 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
The light waves from two coherent sources have same intensity I1=I2=I0. In interference pattern the intensity of light at minima is zero. What will be the intensity of light at maxima ?
View Solution1800 waves are passing through a point in 2 minutes in a medium. What will be the wavelength if the speed of wave in the medium is 900 m/s ?
View Solution
Knowledge Check
If the frequency of a wave is 330 Hz, and velocity of wave in air is 330 m s−1, then, the wavelength of the wave is
A0.5 mB1 mC2 mDnot certainIf the velocity of a wave is 400 m/sec and frequency is 100 Hz, then the wavelength of the wave is _______
A6 mB2.8 mC3 mD4 m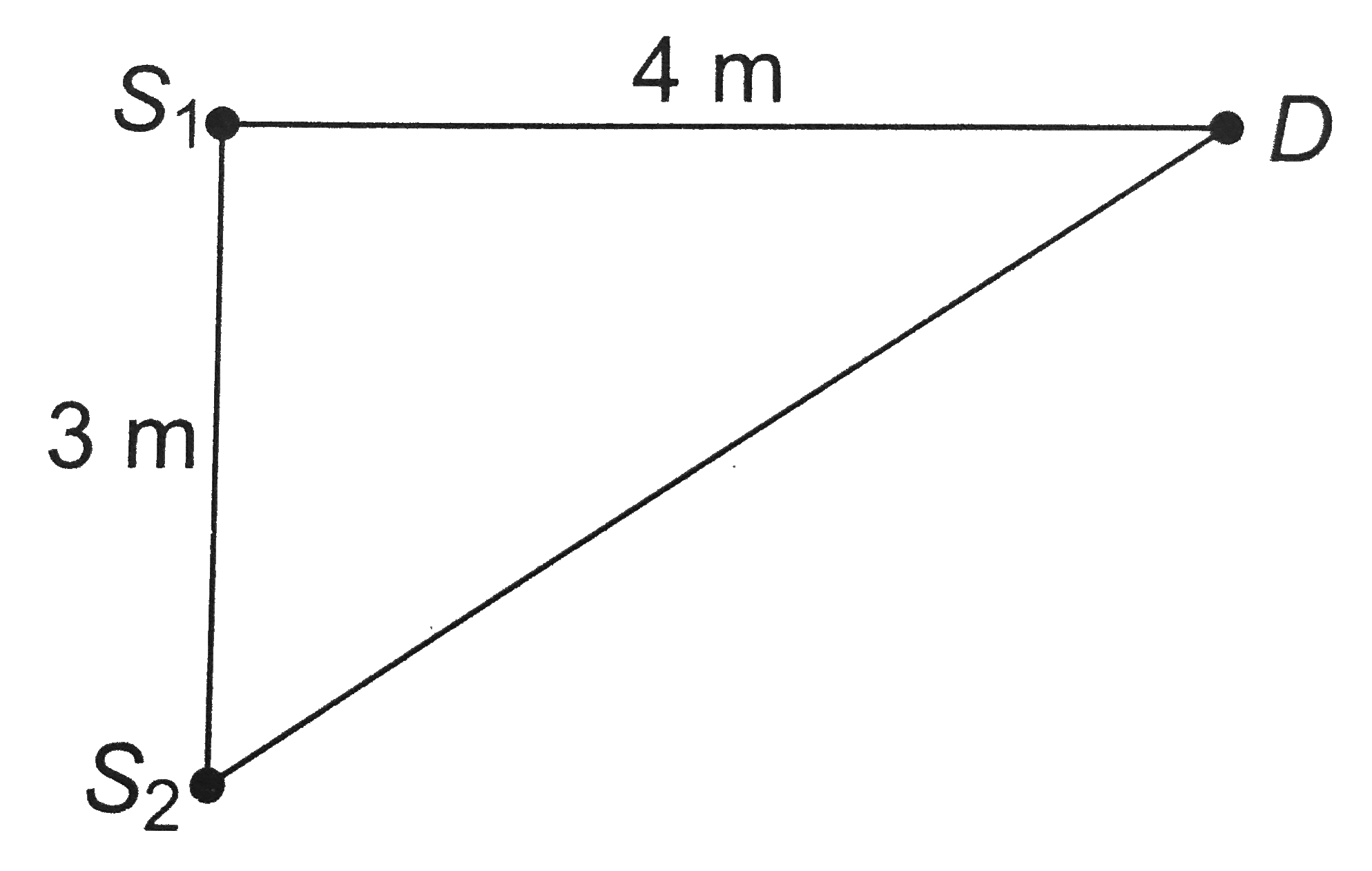
In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0Dzero
Calculate the wavelength of a sound wave whose frequency is 220Hz and speed is 440m/s in a given medium.
View SolutionThe unit of intensity of a wave is Wm2? What are dimensions of intensity of wave?
View SolutionA sound source emits sound waves of 400 Hz. It produces waves of wavelength 2.5 m. The velocity of sound waves is
View SolutionThe velocity of a wave is 220ms−1, the distance travelled by the wave in 2s is __________ m
View SolutionThe phase difference between two points separated by 0.8 m in a wave of frequency 120 Hz is 0.5π. The velocity of wave will be
View Solution
