Three bodies of equal masses are placed at (0,0) ,(a,0) and (a2.a√32) . Find out the cordinates of centre of mass .
(a2,a√36)
(a,a2)
(√3a6,a)
(a2,a2)
The correct Answer is:A
To find the coordinates of the center of mass of three bodies placed at the given coordinates, we can follow these steps:
Step 1: Identify the coordinates and masses
We have three bodies with equal masses m located at the following coordinates:
1. Body 1: (0,0)
2. Body 2: (a,0)
3. Body 3: (a2,a√32)
Step 2: Use the center of mass formula
The formula for the center of mass (xcm,ycm) for a system of particles is given by:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Since all masses are equal, we can denote the mass of each body as m.
Step 3: Calculate xcm
Substituting the coordinates into the formula for xcm:
xcm=m⋅0+m⋅a+m⋅a2m+m+m
=0+a+a23m
=a+a23
=2a2+a23=3a23=a2
Step 4: Calculate ycm
Now, substituting the coordinates into the formula for ycm:
ycm=m⋅0+m⋅0+m⋅a√32m+m+m
=0+0+a√323m
=a√323=a√36
Step 5: Final coordinates of the center of mass
Thus, the coordinates of the center of mass are:
(a2,a√36)
Summary
The center of mass of the three bodies is located at:
(a2,a√36)
We have three bodies with equal masses m located at the following coordinates:
1. Body 1: (0,0)
2. Body 2: (a,0)
3. Body 3: (a2,a√32)
The formula for the center of mass (xcm,ycm) for a system of particles is given by:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Since all masses are equal, we can denote the mass of each body as m.
Substituting the coordinates into the formula for xcm:
xcm=m⋅0+m⋅a+m⋅a2m+m+m
=0+a+a23m
=a+a23
=2a2+a23=3a23=a2
Now, substituting the coordinates into the formula for ycm:
ycm=m⋅0+m⋅0+m⋅a√32m+m+m
=0+0+a√323m
=a√323=a√36
Thus, the coordinates of the center of mass are:
(a2,a√36)
The center of mass of the three bodies is located at:
(a2,a√36)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 2
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Four particles of masses m,2m,3m,4m are placed at corners of a square of side 'a' as shown in fig. Find out coordinateds of centre of mass.
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View Solution
Knowledge Check
Vertics of a triangle ABC are the points (0,0),(a,0) and (a2,a√32). Its incentre is the point
A(3a4,√3a4)B(a2,a√36)C(a6,a√32)D(a3,a√32)Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of these
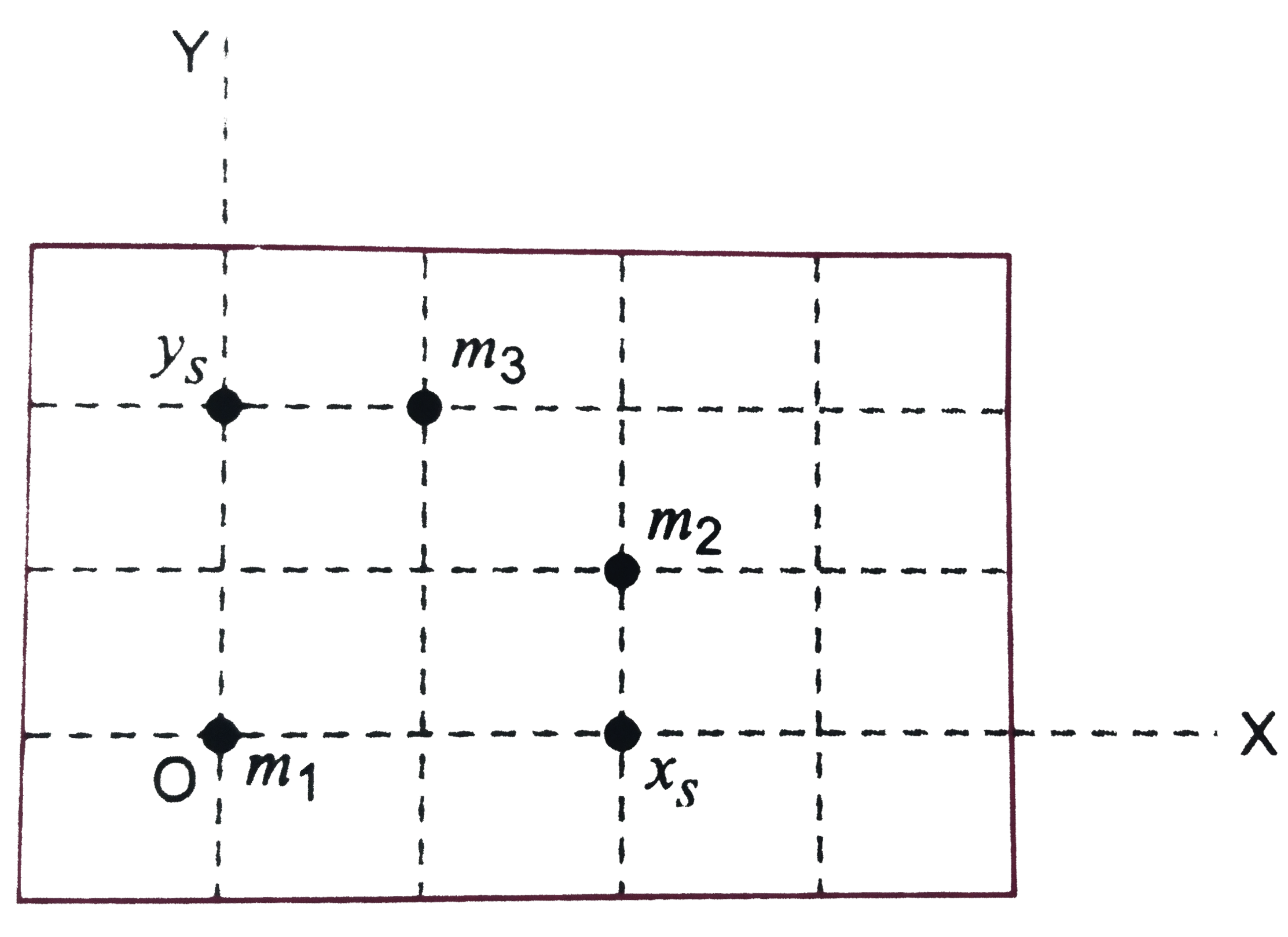
Fig. shown a three particle system with masses m1=3.0kg,m2=4.0kg and m3=8.0kg. The scales on the axes are set by xs=2.0m and ys=2.0m. What are the co-ordinates of centre if mass ? If m3 is gradually increased, does the centre of mass of the system shift towards or away from that particle or does it remain stationary ?
View SolutionIf three vertices of a rectangle or (0,0), (2,0)and(0, 3), find the coordinates of the fourth vertex.
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionTwo particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
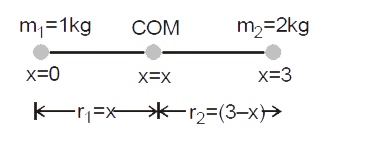
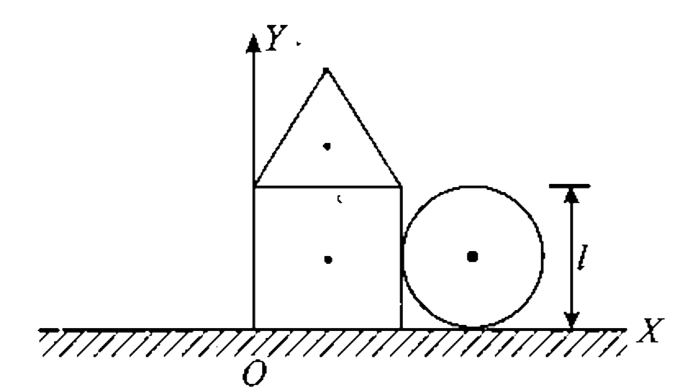
View SolutionThree laminar bojects of uniform density a square, a disc and an equilateral triagle are placed as shown fig. find the coordinates of centre of mass of the three bodies.
View SolutionThree point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View Solution
