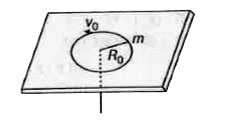
m द्रव्यमान का एक पिण्ड ( वस्तु ), R0 त्रिज्या के पथ में किसी चिकने क्षैतिज समतल के ऊपर v0 वेग से गति कर रहा है | यह पिण्ड एक डोरी ( रस्सी ) से जुड़ा है | यह डोरी समतल पर बने एक चिकने छिद्र से होकर गुजरती है जैसा कि आरेख में दर्शाया गया है | इस डोरी पर तनाव को धीरे - धीरे बढ़ाया जाता है, जिससे अंत में यह पिण्ड R02 त्रिज्या के वृत्ताकार पथ पर गति करने लगता है , तो गतिज ऊर्जा का अंतिम मान है
mv20
14mv20
2mv20
12mv20
The correct Answer is:C
दिया गया है, प्रारम्भिक पथ की त्रिज्या =R0
अन्त में पथ की त्रिज्या =R02
प्रारम्भ में वस्तु का वेग =v0
कोणीय संवेग संरक्षण के सिद्धान्त से,
Li=Ll⇒mv0R0=mv.(R02)
⇒ v.=2v0
अतः कण की अन्तिम गतिज ऊर्जा,
Kt=12mv.2=12m(2v0)2
=4×12mv20=2mv20
Topper's Solved these Questions
Similar Questions
एक m द्रव्यमान तथा r त्रिज्या कि रिंग केंद्र से गुजरने वाले अक्ष के लम्बवत घूमती है। इसका कोणीय वेग ω है। इसकी गतिज ऊर्जा होगी :
View Solutionएक पूर्ण प्रत्यास्थ पिण्ड के लिए प्रत्यावस्थान गुणांक का (coefficient of restitution ) मान है :
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionकिसी समतल में गति | किसी समतल में एक समान त्वरण से गति | दो विमाओं में आपेक्षिक वेग
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक ठोस यौगिक X को गर्म करने पर यह CO2 गैस और एक अवशिष्ट देता है। अवशिष्ट जल के साथ मिश्रित होकर Y बनाता है। जल में Y के माध्यम से CO2 आधिक्य को गुजारने पर एक स्वच्छ विलयन Z प्राप्त होता है। Z को उबलने पर, यौगिक X का पुनः निर्माण होता है। यौगिक X है
View Solution
