Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
mutually exclusive and independent
equally likely but not independent
Independent but not equally likely
independent and equally likely
The correct Answer is:C
P(¯¯¯¯¯¯¯¯¯¯A∪B)=16
P(A∪B)=56,P(A)=34
P(A∪B)−P(A)+P(B)−P(A∩B)=56
⇒P(B)=56−34+14=13
⇒P(A∩B)=P(A).P(B)=14
Topper's Solved these Questions
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:JEE Advanced Previous Year
Explore 25 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:LINKED COMPREHENSION TYPE
Explore 11 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:Exercise (Numerical)
Explore 20 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:JEE Advanced Previous Year
Explore 7 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
Similar Questions
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14 where ¯¯¯A stands for complement of event A. Then, events A and B are
View SolutionLet A and B be two events such that
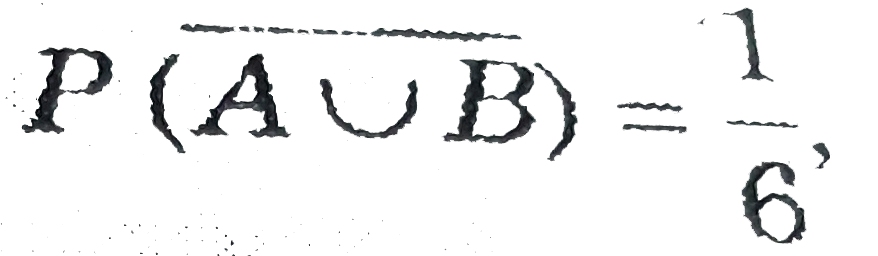 ,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are
,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are
View Solution
Knowledge Check
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCindependent but not equally likelyDindependent and equally likelyLet A and B be two events such that p(¯¯¯A∪B)=16,p(A∩B)=14 and p(¯¯¯A)=14 , where ¯¯¯A stands for the complement of the event A. Then the events A and B are (1) mutually exclusive and independent (2) equally likely but not independent (3) independent but not equally likely (4) independent and equally likely
Amutually exclusive and independentBequally likely but not independentCIndependent but not equally likelyDindependent and equally likelyIf A and B are two events such that P(A∪B)=34, P(A∩B)=14,P(¯¯¯A)=23, then
AP(¯¯¯A∩B)=512BP(B)=23CP(¯¯¯A∪¯¯¯B)=14DP(¯¯¯A∪¯¯¯B)=34
If A and B are two events such that P((A ∪ B)')=16,P(A∩B)=14 and P(A')=14, then P(A) and P(B) are
View SolutionLet A and B be the two events such that P(A)=12,P(B)=13andP(A∩B)=14 , find
P(AB)
View SolutionIf A and B are two events such that P[(A∪B)']=16,P(A∩B)=14 and P(A')=14 , then events A and B are
View SolutionLet A and B be two events such that
P(A∩B)=16,P(A∪B)=3145 and P(¯¯¯B)=710, then
View SolutionIf A and B are any two events such that P(A∪B)=34,
P(A∩B)=14andP(¯¯¯A)=23, where ¯¯¯A stands for the complementary event of A, then what is P(B) ?
View Solution

