A charge q is placed at the point of intersection of body diagonals of a cube. The electric flux passing through any one of its face is
The correct Answer is:A, C
To find the electric flux passing through one face of a cube when a charge q is placed at the intersection of the body diagonals, we can use Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand the Geometry of the Cube
The charge q is located at the center of the cube, which is the point of intersection of the body diagonals. A cube has 6 faces.
Hint: Visualize the cube and the position of the charge at its center.
Step 2: Apply Gauss's Law
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
Hint: Remember that Gauss's Law applies to closed surfaces.
Step 3: Calculate the Total Electric Flux
Since the charge q is enclosed within the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Hint: Consider the symmetry of the cube; the charge is at the center.
Step 4: Determine the Flux Through One Face
Since the cube has 6 identical faces, the electric flux through one face can be found by dividing the total flux by the number of faces:
Φone face=Φtotal6=q6ϵ0
Hint: Think about how the total flux is evenly distributed among all faces of the cube.
Final Answer
Thus, the electric flux passing through any one of the faces of the cube is:
Φ=q6ϵ0
The charge q is located at the center of the cube, which is the point of intersection of the body diagonals. A cube has 6 faces.
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
Since the charge q is enclosed within the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Since the cube has 6 identical faces, the electric flux through one face can be found by dividing the total flux by the number of faces:
Φone face=Φtotal6=q6ϵ0
Thus, the electric flux passing through any one of the faces of the cube is:
Φ=q6ϵ0
Topper's Solved these Questions
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION B
Explore 9 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION C
Explore 8 Videos
- QUESTION PAPER 2023Book:XII BOARDS PREVIOUS YEARChapter:QUESTION PAPER 2023Exercise:Question
Explore 43 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SECTION - B
Explore 9 Videos
Similar Questions
Knowledge Check
A charge 4μC is located at the centre of one of the edge of a cube . The electric flux through the cube is (all quantities are in SI units)
A4×10−6ε0B10−6ε0C2×10−6ε0DZeroA point charge Q is placed at one of the vertices of a cubical block. The electric flux flowing through this cube is
AQ6ε0BQ4ε0CQ8ε0DQε0A charge q is located at the centre of a cube. The electric flux through any face is
Aπq6(4π∈0)Bq6(4π∈0)C2πq6(4π∈0)D4πq6(4π∈0)
Point charge Q is placed at point P in the plane of circular face of sphere. The electric flux passing through the spherical part shown in the figure is:-
View SolutionA point charge Q is placed at the centre of a hemisphere. Find the ratio of electric flux passing through curved andplane surface of the hemisphere.
View SolutionA charge q is placed at the centre of a hollow sphere of radius r, Total electric flux passing through the spherical surface is __________
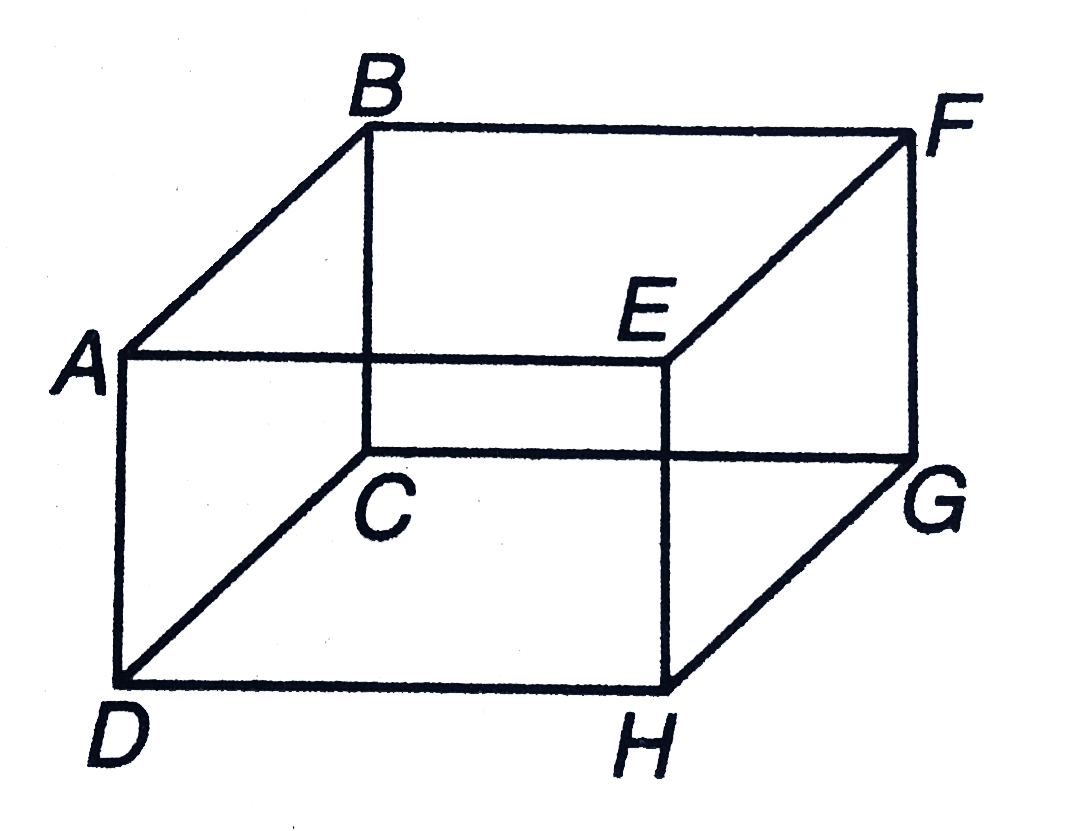
View SolutionA charge q is placed at point D of the cube. Find the electric flux passing through the EFGH and face AEHD.
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View Solution

