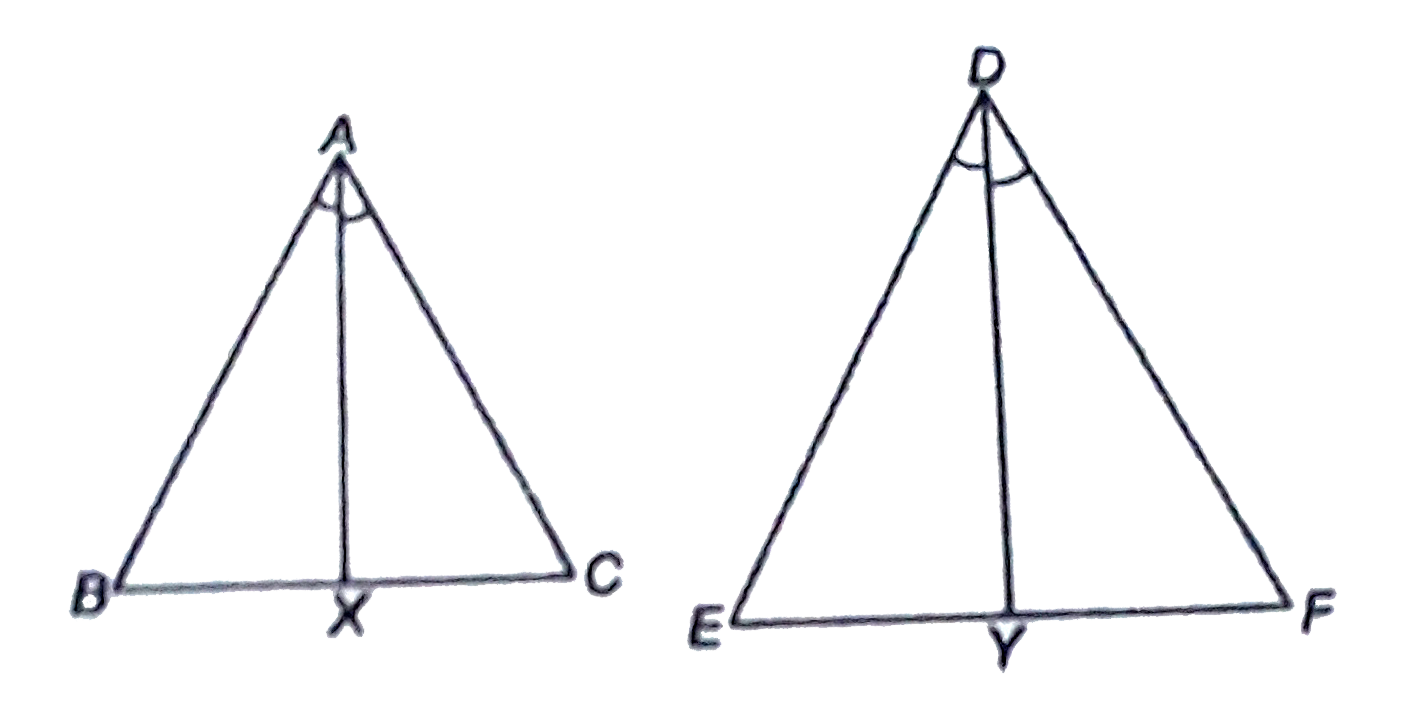
If two triangles are similar; prove that the ratio of the corresponding sides is same as the corresponding angle bisector segments.

Video Solution

Text Solution

Verified by Experts

Given : $△ A B C ~ △ D E F$ in which AX and DY are the bisectors of $∠ A and ∠ D$ respectively.
To prove: $\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A B^{2}}{D E^{2}}$
Proof: Given $△ A B C ~ △ D E F$
Therefore, $∠ A = ∠ D$
$\Rightarrow \frac{1}{2} ∠ A = \frac{1}{2} ∠ D$
Now, in $△ A B X and △ D E Y$ , we have
$∠ B A X = ∠ E D Y$
and $∠ B = ∠ E$
$△ A B X ~ △ D E Y$ (by AA similartiy)
Hence $\frac{A B}{D E} = \frac{A X}{D Y}$ ...(1) (given)
Now ,in $△ A B C and △ D E F$
$△ A B C ~ △ D E F$
therefore, $\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A B^{2}}{D E^{2}}$ ....(2)
( in similar triangles the ratio of areas of triangles is equal to ratio of squares of their corresponding sides)
form (1) and (2) , we have
$\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A X^{2}}{D Y^{2}}$

Updated on:21/07/2023

If area of two similar triangle are equal then ratio of their corresponding altitude is.
A $1 : 1$
B $1 : \sqrt{2}$
C $1 : 2$
DCannot be determined
Area of two similar triangles are in the ratio of 5:3 then the ratio of their corresponding sides is :
A $5 : 3$
B $25 : 9$
C $9 : 25$
D $\sqrt{5} : \sqrt{3}$
If the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
A $2 : 3 : 1$
B $\sqrt{3} : 2 : 1$
C $2 : \sqrt{3} : 1$
D $1 : \sqrt{3} : 2$