If two triangles are similar; prove that the ratio of corresponding sides is equal to the ratio of corresponding altitudes.

Video Solution

Text Solution

Verified by Experts

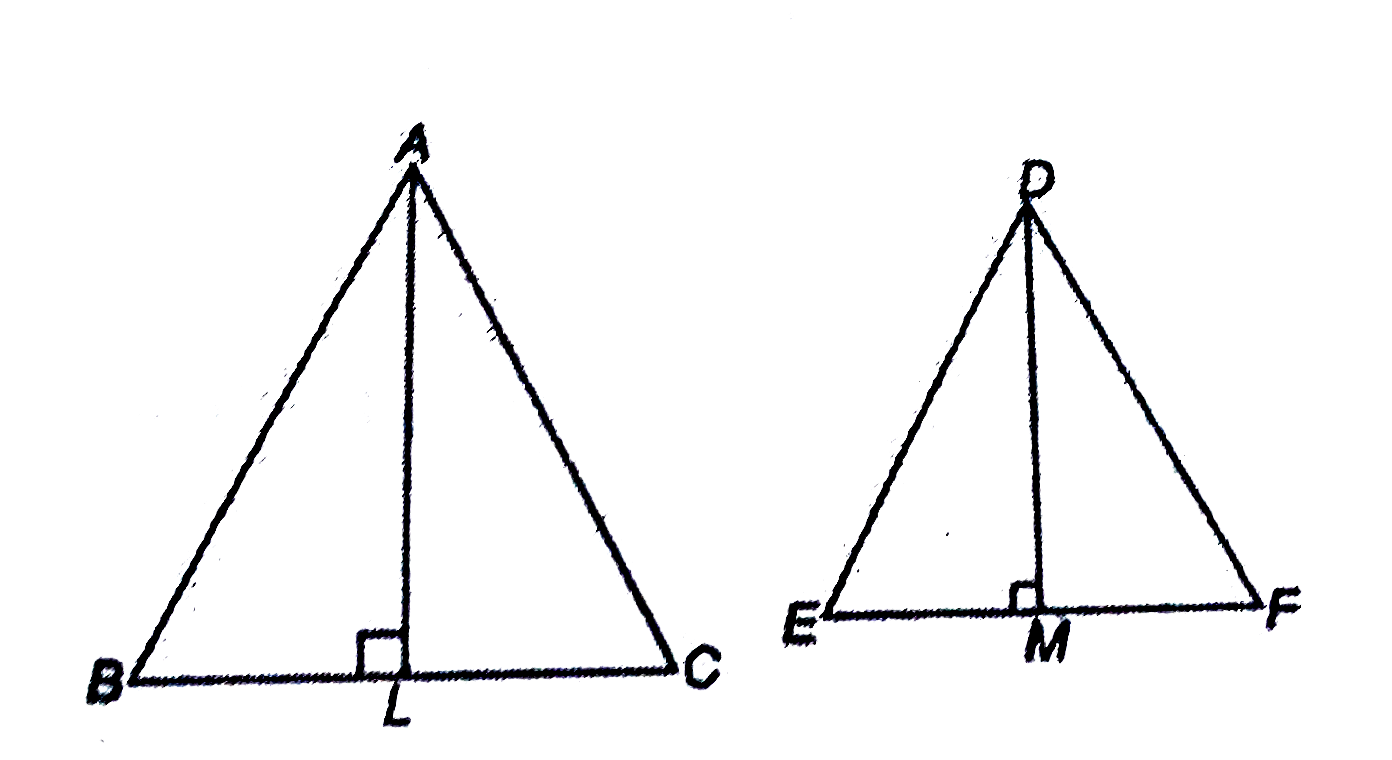
Given : $△ A B C ~ △ D E F A L ⊥ B C and D M ⊥ E F$
To prove : $\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A L^{2}}{D M^{2}}$
proof: in $△ A L B and △ D M E$ ,
$∠ B = ∠ E (g i v e n △ A B C ~ △ D E F)$
$∠ A L B = ∠ D M E = 90^{\circ}$ (each)
$△ A B L ~ △ D E M$ (by AA similarity)
$\Rightarrow \frac{A B}{D E} = \frac{A L}{D M} . . (1)$
Now , $\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A B^{2}}{D E^{2}} ... (2)$
( the ratio of areas of two similar triangles is equal to ratio of squares of the corresponding sides)
Form (1) and (2) we have
$\frac{a r (△ A B C)}{a r (△ D E F)} = \frac{A L^{2}}{D M^{2}}$ Hence proved.

Updated on:21/07/2023

If area of two similar triangle are equal then ratio of their corresponding altitude is.
A $1 : 1$
B $1 : \sqrt{2}$
C $1 : 2$
DCannot be determined
If the ratio of the altitudes of two triangles be 3:4 and the ratio of their corresponding areas be 4 : 3, then the ratio of their corresonding lengths of bases is
A $1 : 1$
B $16 : 9$
C $1 : 2$
D $2 : 1$
If the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
A $2 : 3 : 1$
B $\sqrt{3} : 2 : 1$
C $2 : \sqrt{3} : 1$
D $1 : \sqrt{3} : 2$