ABC
is an isosceles triangle with AB=AC
and D
is a point on AC
such that BC2=AC×CD.
Prove that BD=BC
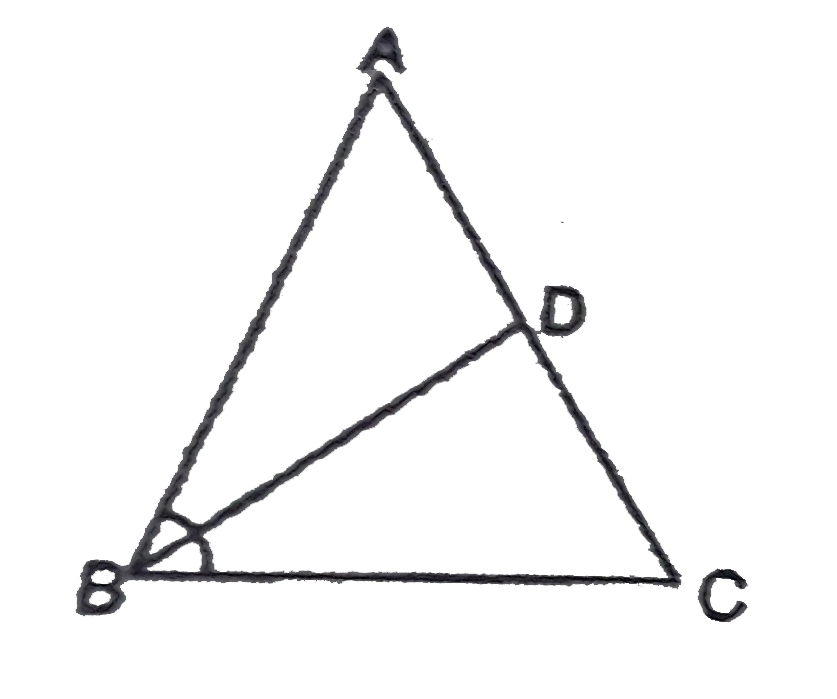
we have
BC2=AC×CDandAB=AC
BC×BC=AC×CDand∠B=∠C
There may be 3 possibilities:

⇒△BCD~△ABC ( by SAS criterion)
BCAB=CDBC=BDAC
BCAB=BDAC
BC=BD (AB= AC, given) Hence proved
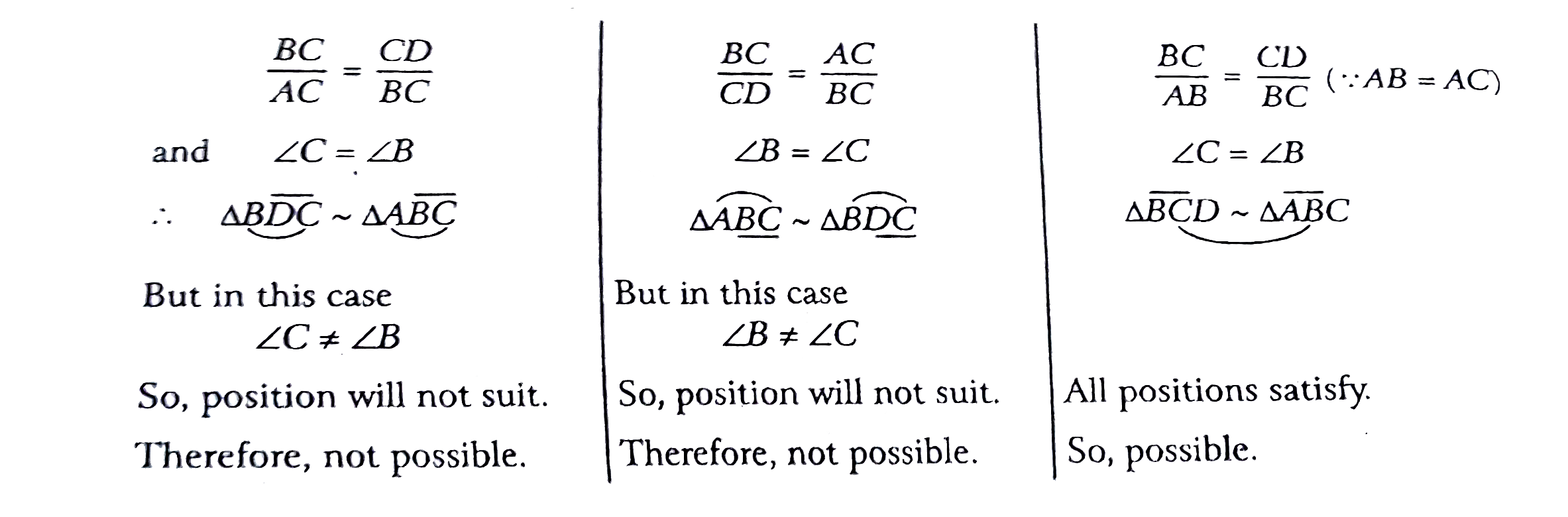
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
ABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
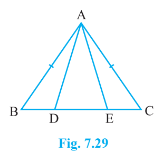
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View Solution
