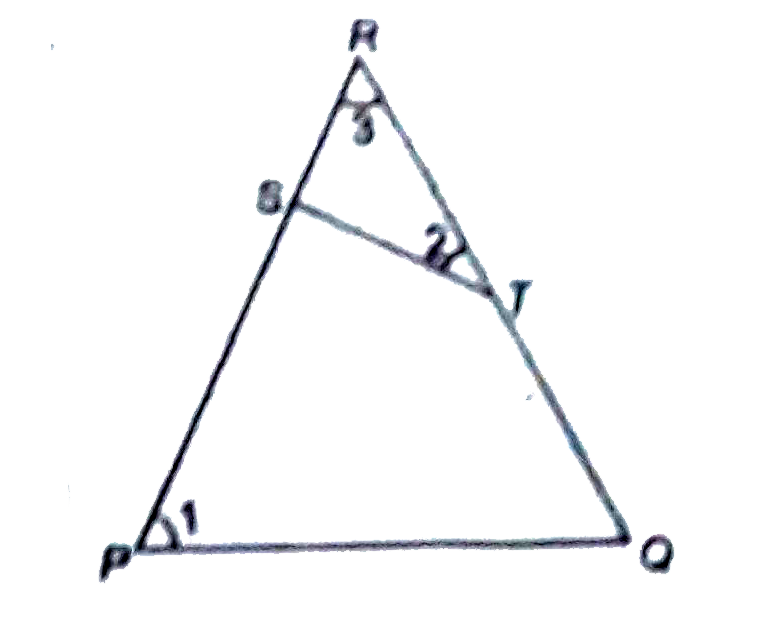
S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS then
RP=RT
PQ=TS
△RPQ~△RTS
QR=RS
The correct Answer is:C
Given : △RPQand△RTSin which∠P=∠RTS
To Prove: △RPQ~△RTS
Proof: In △RPQand△RTS we, have
∠1=∠2 (given)
∠3=∠3 ( common)
 (by AA corollary)
(by AA corollary)
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
S and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.

View SolutionIn the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.

View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
View SolutionIf S is a point on side PQ of a △PQR such that PS = QS = RS, then PR2+QR2 = ……………..
View SolutionS in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
View SolutionA and Bare respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 10.5 m PA = 4.5 m, BR= 8 m and PB= 6 m. Is AB||QR?
View Solution
