A body with an initial velocity u and a uniform acceleration, covers a distance s in time t and acquires a velocity v. Compare the velocity of the body at half at half of the distance covered with the velocity at half of the total time of travel. Solution in Bengali
Let the acceleration of the body be a.
v = u+at
Velocity at half of the total time of travel,
Also,
Velocity at half of the distance covered,
Now,
which is a negative quantity. Hence , i.e., the velocity of the body at half-distance is greater than the velocity at half-time.
Topper's Solved these Questions
- ONE - DIMENSIONAL MOTION Book:CHHAYA PUBLICATIONChapter:ONE - DIMENSIONAL MOTION Exercise:EXERCISE (Multiple Choice Questions)
Explore 31 Videos
- ONE - DIMENSIONAL MOTION Book:CHHAYA PUBLICATIONChapter:ONE - DIMENSIONAL MOTION Exercise:EXERCISE ( Graphical Analysis )
Explore 1 Video
- ONE - DIMENSIONAL MOTION Book:CHHAYA PUBLICATIONChapter:ONE - DIMENSIONAL MOTION Exercise:Section Related Questions
Explore 17 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBook:CHHAYA PUBLICATIONChapter:NEWTONIAN GRAVITATION AND PLANETARY MOTIONExercise:CBSE SCANNER
Explore 19 Videos
- QUESTION PAPERS OF NEET -2017Book:CHHAYA PUBLICATIONChapter:QUESTION PAPERS OF NEET -2017Exercise:QUESTION
Explore 32 Videos
Similar Questions
A vehicle is moving with a uniform speed of 18 km.h−1 . The distance covered by it in 1 s is
View SolutionFor a freely falling body the acceleration graph is -
(A) Straight line parallel to the acceleration axis.
(B) Straight line parallel ot the time axis.
(C) Straight line passing through the origin.
(D) Parabola passing through the origin.
View SolutionDefine rest and motion.
View SolutionWhat is the reason for absence of atmosphere in some planets?
View SolutionA molecule of a substance has permanent dipole moment p . A mole of this substance is polarised by applying a storg electrostatic field E . The direction of the field is suddenly changed of 60∘ . If N is the avogadro's number the amount of work done by the field is
View SolutionRefering to v−s diagram, find:
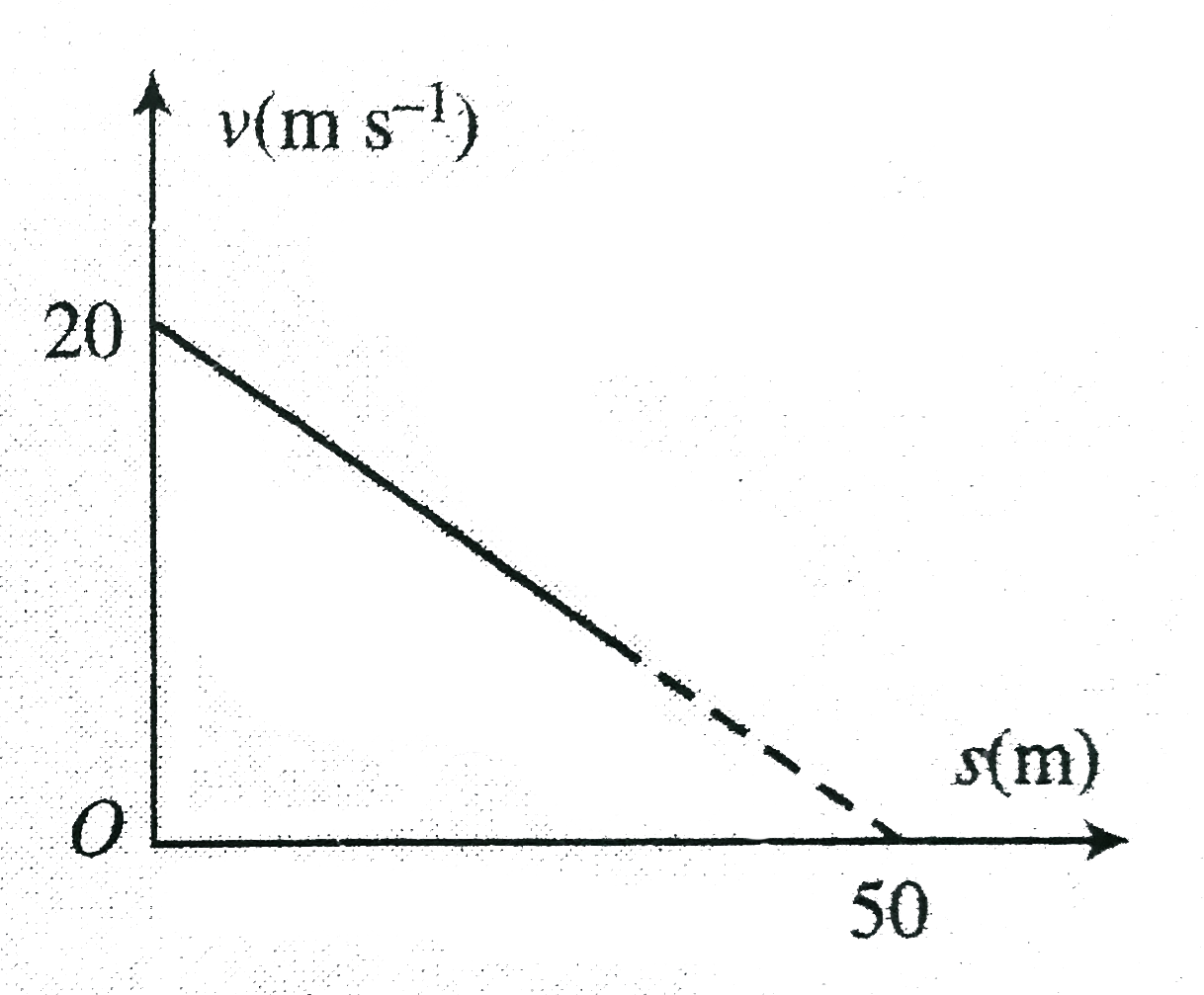 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.
View SolutionA cae is travelling along a straight line. It covers one-half of the total, distance with a velocity 10 km//h . The remaining part of the distance was covered with velocity 12 ms^(-1) . For half the time and with velocity 16 ms^(-1) for the other half the tiem. Find the average speed over the whole time of motion.
View SolutionA point traversed half the distance with a velocity v0. The remaining part of the distance was covered with velocity v1 for half the time, and with velocity v2 for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
View SolutionA body travelling along a straight line traversed one third of the total distance with a velocity 4m/s. The remaining part of the distance was covered with a velocity 1 m/s for half the time and with velocity 3 m/s for the other half of time. The mean velocity averaged over the whole time of motion is :
View SolutionA body covers half the distance with a velocity 10 m/s and remaining half with a velocity 15 m/s along a straight line. The average velocity will be-
View SolutionA body covers half the distance with a velocity 10 m/ s and remaining half with a velocity 15 m/s along a straight line. The average velocity will be-
View SolutionA point travelled half of the distance with velocity v0. The half of remaining part of the distance was covered with velocity v1 & second half of remaining part by v2 velocity. The mean value of the point averaged over the whole time of motion is
View SolutionThe initial velocity is u and acceleration (f) is uniform. Final velocity and distance covered in the interval t are v and s respectively. Show that the velocity of the particle at half-distance is more than the velocity for half -time.
View SolutionA car completes the first half of its journey with a velocity υ1 and the rest half with a velocity υ2. Then the average velocity of the car for the whole journey is :
View SolutionA particle is moving in a straight line. It covers half of the total distance with velocity v_(0) Remaining half distance is covered with a velocity v_(1) for half the time and with velocity v_(2) for another half of time. Find the average velocity of the particle.
View SolutionA particle traversed half of the distance with a velocity of V_0 . The remaining parts of the distance was covered with velocity V_1 for half of the time and with V_2 for other half of the time. Find the mean velocity of the particle averaged and the whole time of motion
View Solution

