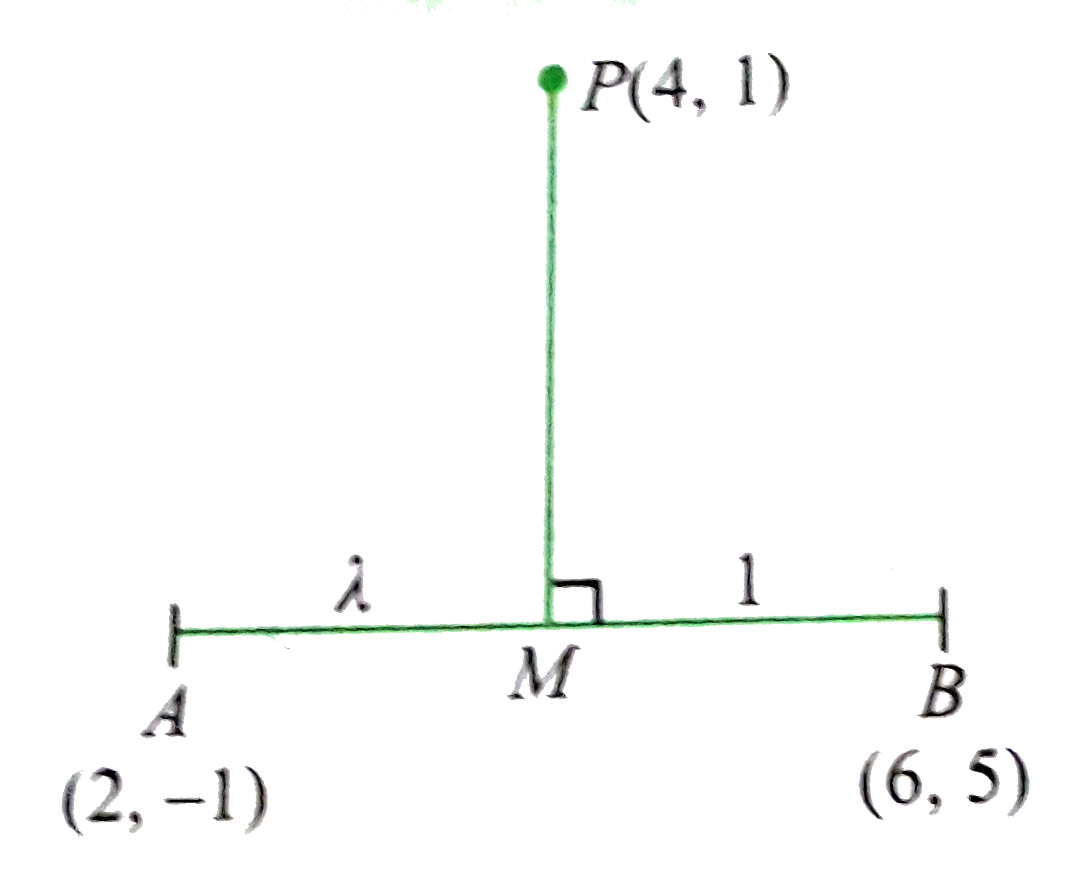
If A(2,-1)a n dB(6,5) are two points, then find the ratio in which t

If A(1, 2, 3), B(4, 5, 6) are two points, then the foot of the perpendicular from point B to the line joining the origin and point A is
A $(\frac{8}{7}, \frac{16}{7}, \frac{24}{7})$
B $(\frac{16}{7}, \frac{32}{7}, \frac{48}{7})$
C $(\frac{1}{7}, \frac{2}{7}, \frac{3}{7})$
D $(\frac{4}{7}, \frac{8}{7}, \frac{12}{7})$
Find the ratio in which the point P(x, 2) divides the join of A(12, 5) and B(4, -3).
A5 : 3
B3 : 5
C1 : 3
D3 : 2
What is the ratio in which point P(1, 2) divides the join of A(-2, 1) and B(7,4)?
A $1 : 2$
B $2 : 1$
C $3 : 4$
D $2 : 3$

If $A (2, - 1) a n d B (6, 5)$ are two points, then find the ratio in which the food of the perpendicular from $(4, 1)$ to $A B$ divides it.