Ifp>q>0andpr<−1<qr, then find the value of tan−1(p−q)1+pq+tan−1(q−r)1+qr+tan−1(r−p)1+rp.
since p,q>0, we have pq>0
tan−1(p−q)1+pq=tan−1p−tan−1q....(i)
Since qr>−1, we have
tan−1(q−r)1+qr=tan−1q−tan−1r...(ii)
Since pr<−1andr<0, we have
tan−1(r−p)1+rp=π+tan−1t−tan−1p....(iii)
On adding Eqs. (i), (ii), and (iii), we get
tan−1(p−q)1+pq+tan−1(q−r)1+qr+tan−1(r−p)1+rp=π
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.1
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.2
6 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
If p>qandr<0 , then which is true? (a) pr < qr (b) p r < q r (c) p + r < q + r (d) None of these
View SolutionIf a,bandc are in A.P., and pandp' are respectively, A.M. and G.M. between aandbwhileq,q' are , respectively, the A.M. and G.M. between bandc, then p2+q2=p'2+q'2 b. pq=p'q' c. p2−q2=p'2−q'2 d. none of these
View Solution
Knowledge Check
If rthand(r+1)th terms in the expansion of (p+q)n are equal, then (n+1)qr(p+q) is
A12B14C1D0If roots of the equation (q−r)x2+(r−p)x+(p−q)=0 are equal, then p,q and r are in
AAPBGPCHPDAGP
If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
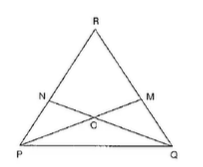
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionIf p, q, r are not in G.P. and ∣∣ ∣ ∣∣1qpα+qp1rpα+rqpα+qqα+r0∣∣ ∣ ∣∣=0 Show that pα2+2qα+r=0
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIf rth and (r+1)th term in the expansion of (p+q)n are equal, then (n+1)qr(p+q) is
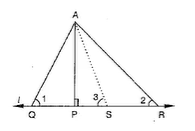
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
View Solution
