(A-B) ∪ (A-C)= ……………..Solution in Telugu
(A-B) ∪C
(A-B)∩ C
(A-B)-C
None
The correct Answer is:D
Step by step video, text & image solution for (A-B) cup (A-C)= …………….. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS Book:VGS PUBLICATION-BRILLIANTChapter:SETS Exercise:OBSERVATION BITS TO SOLVE VARIOUS QUESTION GIVEN IN THE PUBLIC EXAMINATION
Explore 21 Videos
- REAL NUMBERS (MULTIPLE CHOICE QUESTION)Book:VGS PUBLICATION-BRILLIANTChapter:REAL NUMBERS (MULTIPLE CHOICE QUESTION)Exercise:REAL NUMBERS (MULTIPLE CHOICE QUESTION)
Explore 22 Videos
- SIMILAR TRIANGLES Book:VGS PUBLICATION-BRILLIANTChapter:SIMILAR TRIANGLES Exercise:CREATIVE BITS FOR CCE MODEL EXAMINATION
Explore 90 Videos
Similar Questions
Set of human being that reside on moon is ………………..
View Solution915=…………..
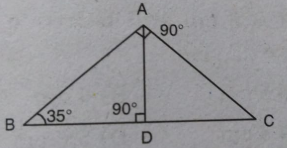
View SolutionFrom the figure ,∠DAC……….
View SolutionIf A={1,2,3,4},B={3,4,5,6},C={5,6,7,8}andD={7,8,9,10}, find :
(i) A∪B
(ii) A∪C
(c) B∪C
(iv) B∪D
(v) A∪B∪C
(vi) A∪B∪D
(vii) B∪C∪D.
View SolutionFor sets A, B,C , show that (A−B)∪(A−C)=A−(B∪C)
View SolutionLet U be the universal set and A∪B∪C=UThen[(A−B)∪(B−C)∪(C−A)]equals
View SolutionIf A={a,b,c,d,e},B={a,c,e,g}andC={b,e,f,g}, verify that:
(i) A∪B=B∪A
(ii)A∪C=C∪A
(iii) B∪C=C∪B
(iv)A∩B=B∩A
(v) B∩C=C∩B
(vi) A∩C=C∩A
(vii) (A∪B)∪CA∪(B∪C)
(viii)A∩C=C∩A .
View SolutionProve A∪(B∩C)=(A∪B)∩(A∪C)
View Solutionयदि A={1,2,3}, B={2,3,4},C={1,3,5}, तो A∪B,A∪C,(A∪B)∪C,(A∪B)∪(A∪C) के मान ज्ञात करो
View Solutionयदि A={2,5,6,7},B={0,2,5,7,8} तथा C={1,2,3,5,6} हो,तो दर्शाइए कि :
A∪(B∩C)=(A∪B)∩(A∪C)
View Solutionयदि A={1,2,3,4}, B={3,4,5,6}, C={5,6,7,8} और D={7,8,9,10}, तो निम्नलिखित ज्ञात कीजिए:
(i) A∪B, (ii) A∪C, (iii) B∪C, (iv) B∪D, (v) A∪B∪C, (vi) A∪B∪D, (vii) B∪C∪D
View Solutionদেখাও যে,(A∪B)\C=(A\C)∪(B\C)
View Solutionयदि U समष्टीय समुच्चय है तथा A∪B∪C=U , तब {(A−B)∪(B−C)∪(C−A)} ' =
View SolutionFor sets A, B,C , show that (A−B)∪(A−C)=A−(B∪C)
View SolutionLet U be the universal set and A∪B∪C=UThen[(A−B)∪(B−C)∪(C−A)]equals
View SolutionSuppose A, B and C are sets, then prove that: A cup (B cap C) = (A cup B) cap (A cup C)
View Solution

