A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also find the rate of the canvas with 500 per
To solve the problem step by step, we need to find the total surface area of the tent, which consists of a cylindrical part and a conical top.
Step 1: Identify the dimensions
- Height of the cylindrical part (h) = 2.1 m
- Diameter of the cylindrical part = 4 m
- Radius of the cylindrical part (R) = Diameter/2 = 4 m / 2 = 2 m
- Slant height of the conical part (l) = 2.8 m
Step 2: Calculate the curved surface area of the cylindrical part
The formula for the curved surface area (CSA) of a cylinder is:
CSAcylinder=2πRh
Substituting the values:
CSAcylinder=2×227×2×2.1
Step 3: Calculate the CSA of the cylindrical part
Calculating:
CSAcylinder=2×227×2×2.1
=887×2.1
=88×2.17
=184.87
=26.4m2
Step 4: Calculate the curved surface area of the conical part
The formula for the curved surface area of a cone is:
CSAcone=πRl
Substituting the values:
CSAcone=227×2×2.8
Step 5: Calculate the CSA of the conical part
Calculating:
CSAcone=227×2×2.8
=22×5.67
=123.27
=17.6m2
Step 6: Calculate the total surface area of the tent
Now, we add the curved surface areas of the cylindrical and conical parts:
Total CSA=CSAcylinder+CSAcone
=26.4+17.6
=44m2
Step 7: Calculate the cost of the canvas
The cost of the canvas can be calculated using the formula:
Cost=Rate×Area
Given the rate is 500 per m²:
Cost=500×44
=22000Rupees
Final Answer:
- The area of the canvas used for making the tent is 44 m².
- The cost of the canvas is 22000 Rupees.
- Height of the cylindrical part (h) = 2.1 m
- Diameter of the cylindrical part = 4 m
- Radius of the cylindrical part (R) = Diameter/2 = 4 m / 2 = 2 m
- Slant height of the conical part (l) = 2.8 m
The formula for the curved surface area (CSA) of a cylinder is:
CSAcylinder=2πRh
Substituting the values:
CSAcylinder=2×227×2×2.1
Calculating:
CSAcylinder=2×227×2×2.1
=887×2.1
=88×2.17
=184.87
=26.4m2
The formula for the curved surface area of a cone is:
CSAcone=πRl
Substituting the values:
CSAcone=227×2×2.8
Calculating:
CSAcone=227×2×2.8
=22×5.67
=123.27
=17.6m2
Now, we add the curved surface areas of the cylindrical and conical parts:
Total CSA=CSAcylinder+CSAcone
=26.4+17.6
=44m2
The cost of the canvas can be calculated using the formula:
Cost=Rate×Area
Given the rate is 500 per m²:
Cost=500×44
=22000Rupees
- The area of the canvas used for making the tent is 44 m².
- The cost of the canvas is 22000 Rupees.
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.4
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
9 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES
14 Videos
Similar Questions
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also find the rate of the canvas with 500 per m2
View SolutionA tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m, and slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of canvas of the tent at the rate of Rs 500 per m2 .
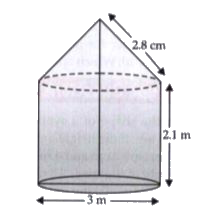
View SolutionIn the figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m , find the area of canvas needed to make the tent. (π=227)
View SolutionIn given figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (Use π=227)

View SolutionIn figure , a tent is in the shape of a cylinder surmounted by a conical top of same diameter . If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m , find the cost of convas needed to make the tent if the canvas is available at the rate of rupees 500/sq.metre .( use π=227)
View SolutionA circus tent is in the shape of a cylinder surmounted by a conical top of same diameter. If their common diameter is 56 cm, the height of cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of canvas used in making the tent
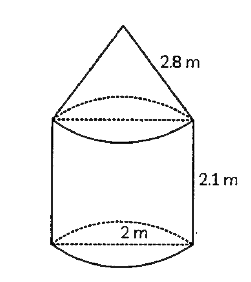
View SolutionIn the figure, a tent is in the shape of a cylinder surmounted by a conical top. The cylindrical part is 2.1 m high and conical part has slant height 2.8 m. Both the parts have same radius 2m. Find the area of the canvas used to make the tent. (Use π=227)
View SolutionA tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24m. The height of the cylindrical portion is 11m while the vertex of the cone is 16m above the ground. Find the area of the canvas required for the tent.
View SolutionA circus tent is cylindrical upto a height of 3m and conical above it. If the diameter of the base is 105m and the slant height of the conical part is 53m, find the total canvas used in making the tent.
View SolutionA tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
View Solution
