Let $O (0, 0), A (2, 0), a n d B (1 \frac{1}{\sqrt{3}})$ be the vertices of a triangle. Let $R$ be the region consisting of all those points $P$ inside $O A B$ which satisfy $d (P, O A) \leq min [d (p, O B), d (P, A B)]$ , where $d$ denotes the distance from the point to the corresponding line. Sketch the region $R$ and find its area.

Video Solution

Text Solution

Verified by Experts

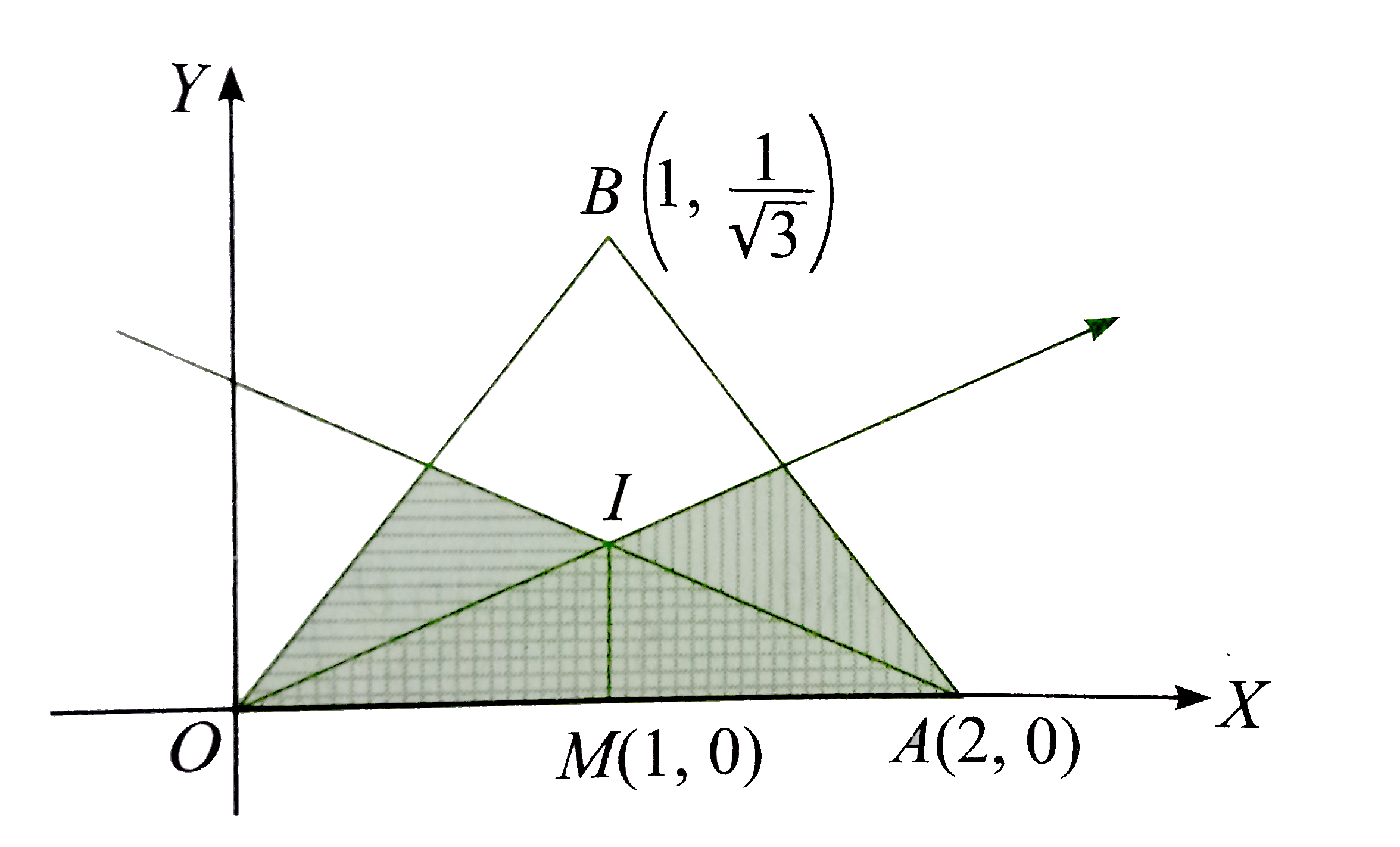
$d (P, O A) \leq min [d (P, O B), d (P, A B)],$
$\Rightarrow d (P, O A) \leq d (P, O B) and d (P, O A) \leq d (P, A B),$
When d(P,OA)= d(P,OB), P is equidistant from OA and OB, i.e., P lies on angle bisector of lines OA and OB.
So, when $d (P, O A) < d (P, O B)$ , Point P is nearer to OA than to OB, i.e., it lies below bisector of OA and oB.
Similarly, when $d (P, O A) < d (P, A B)$ P is nearer to OA than to AB, i.e., it lies below bisector of OA and AB.
Common region satisfied by these two inequalities is the region formed by two bisectors and OA, i.e., triangle OIA.
$∴ Required area = Area of triangle OIA$
$Now, ∠ B O A = \frac{1 / \sqrt{3}}{1} = \frac{1}{\sqrt{3}}$
$∴ ∠ B O A = 30^{\circ}$
$\Rightarrow ∠ I O A = 15^{\circ}$
$\Rightarrow I M = tan 15^{\circ} = 2 - \sqrt{3}$
$∴ Area of triangle OIA = \frac{1}{2} \times O A \times I M$
$= \frac{1}{2} \times 2 \times (2 - \sqrt{3}) = 2 - \sqrt{3} sq. units$

Updated on:21/07/2023

Let O(0, 0) and $B (1, \frac{1}{\sqrt{3}})$ be the vertices of a triangle. Let R be the region consisting of all those points P inside $Δ O A B$ satisfying. $d (P, O A) l r$ min ${d (P, O B), d (P, A B)}$ , where d denotes the distance from the point P to the corresponding line. Let M be peak of region R.
The perimeter of region R is equal to
A $\sqrt{3}$
B $\frac{1}{\sqrt{3}}$
C3
D $2 - \sqrt{3}$
Let $O (0, 0), A (2, 0) and B (1, \frac{1}{\sqrt{3}})$ be the vertices of a triangle. Let R be the region consisting of all those points P inside $Δ O A B$ satisfying. $d (P, O A) l r$ min ${d (P, O B), d (P, A B)}$ , where d denotes the distance from the point P to the corresponding line. Let M be peak of region R. The perimeter of region R is equal to
A $4 - \sqrt{3}$
B $4 + \sqrt{3}$
C $4 + 3 \sqrt{3}$
D $2 + 4 \sqrt{(2 - \sqrt{3})}$
Consider the traingle having vertices $O (0, 0), A (2, 0)$ , and $B (1, \sqrt{3})$ . Also $b \leq min {a_{1}, a_{2}, a_{3} ... . a_{n}}$ means $b \leq a_{1}$ when $a_{1}$ is least, $b \leq a_{2}$ when $a_{2}$ is least, and so on. Form this, we can say $b \leq a_{1}, b \leq a_{2}, ... . . b \leq a_{n}$ .
Let R be the region consisting of all those points P inside $Δ O A B$ which satisfy $d (P, O A) \leq min [d (P, O B), d (P, A B)]$ , where d denotes the distance from the point to the corresponding line. then the area of the region R is
A $\sqrt{3}$ sq,units
B $(2 + \sqrt{3})$ sq.units
C $\sqrt{3} / 2$ sq.units
D $1 / \sqrt{3}$ sq.units