Question

Let ${\displaystyle ABC}$
be a triangle with ${\displaystyle AB=AC\stackrel{.}{}}$
If ${\displaystyle D}$
is the midpoint of ${\displaystyle BC,E}$
is the foot of the perpendicular drawn from ${\displaystyle D}$
to ${\displaystyle AC,andF}$
is the midpoint of ${\displaystyle DE,}$
then prove that ${\displaystyle AF}$
is perpendicular to ${\displaystyle BE\stackrel{.}{}}$

Explanation

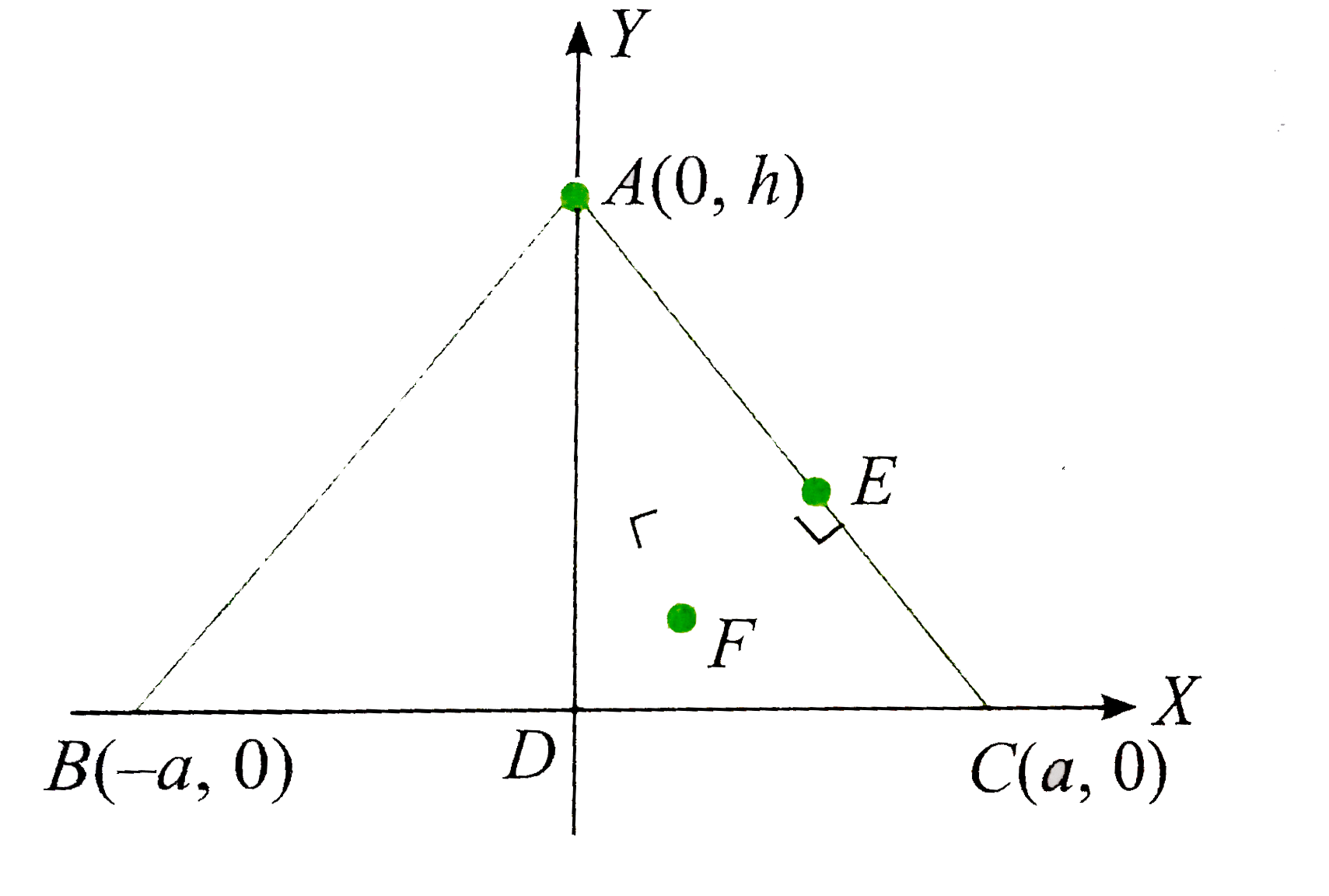
Let BC be taken as the x-axis with the origin at D. Let A be taken on y-axis. Let BC=2a. Now AB=AC, then the coordinates of B and C are (-a,0) and (a,0), respectively. Let DA =h. Then the coordiantes of A are (0,h).
Hene, the equation of AC is ltbgt `(x)/(a)+(y)/(h)=1 " " (1)`
and the equation of DE perpendicular to AC and passing through the origin is
`(x)/(h)-(y)/(a)=0`
`" or " x=(hy)/(a) " " (2)`
Solving (1) and (2), we get the coordinates of E as follows:
`(hy)/(a^(2)) +(y)/(h)=1`
`" or " h^(2)y+a^(2)y = a^(2)h`
`" or " y=(a^(2)h)/(a^(2) + h^(2)) `
`therefore x=(ah)/(a^(2) + h^(2)) `
`therefore E-=((ah^(2))/(a^(2) + h^(2)),(a^(2)h)/(a^(2) + h^(2))) `
Since F is the midpoint of DE, its coordinates are
`((ah^(2))/(2(a^(2) + h^(2))),(a^(2)h)/(2(a^(2) + h^(2)))) `
The slope of AF is
`m_(1) = (h-(a^(2)h)/(2(a^(2)+h^(2))))/(0-(ah^(2))/(2(a^(2)+h^(2))))`
`(2h(a^(2) +h^(2))-a^(2)h)/(-ah^(2)) = (a^(2) + 2h^(2))/(ah) " " (1)`
and the slope of BE is
`m_(2) = ((a^(2)h)/(a^(2)+h^(2))-0)/((ah^(2))/(a^(2)+h^(2)) + a)`
`= (a^(2)h)/(ah^(2)+a^(3)+ah^(2)) = (ah)/(a^(2)+2h^(2)) " " (2)`
From (1) and (2), we have
`m_(1)m_(2) = -1`
` " or " AF bot BE`