In △ABC, vertex A is (1, 2). If the internal angle bisector of ∠B is 2x−y+10=0 and the perpendicular bisector of AC is y = x, then find the equation of BC
The image D of A in the bisector of ∠B lies on BC.
Now, the image of A(1,2) in the line 2x-y-10=0 is given by
x1−12=y1−2−1=−2(2−2+10)4+1
. ∴D(x1,y1)≡D(−7,6)
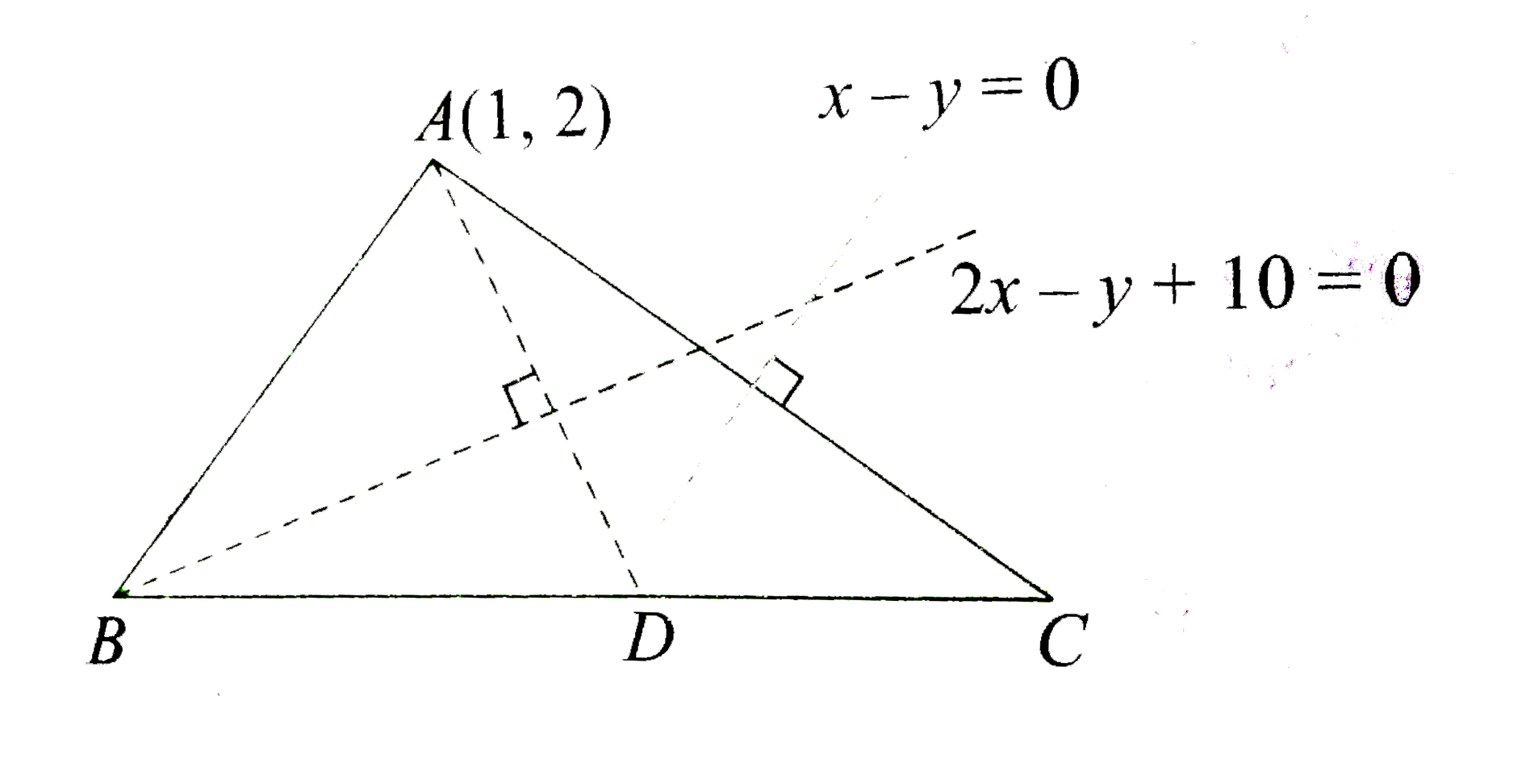
Also, C is the image of A in the perpendicular bisector of AC. The image of A(1,2) in y=x is C(2,1).
Hence the equation of line BC is
. y−1=6−1−7−2(x−2)
or 5x+9y-19=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
In △ABC, vertex A is (1, 2). If the internal angle bisector of ∠B is 2x−y+10=0 and the perpendicular bisector of AC is y = x, then find the equation of BC
View SolutionLet ABC be a triangle and A≡(1,2),y=x be the perpendicular bisector of AB and x−2y+1=0 be the perpendicular bisector of ∠C . If the equation of BC is given by ax+by−5=0 then the value of a−2b is
View Solution
Knowledge Check
The joint equation of bisectors of angles between lines x=5 and y=3 is
A(x−5)(y−3)=0Bx2−y2−10x+6y+16=0Cxy=0Dxy−5x−3y+15=0Let the equations of side BC and the internal angle bisector of angle B of ΔABC are 2x−5y+a=0 and y+x=0 respectively. If A=(2,3), then the value of of a is equal to
A4B2C−2D−4
Let in ΔABC the coordinates of A are (0, 0). Internal angle bisector of ∠ABC is x−y+1=0 and mid - point of BC is (−1,3). Then, the ordinate of C is
View SolutionIn a triangle ABC, A(3,5) is the vertex. If the internal angle bisector of B is y=x then which of the following point must be lie on line BC .
View SolutionLet in ΔABC coordinates of vertex A is (0,0). Equation of the internal angle bisector of ∠ABC is x+y−1=0 and mid-point of BC is (1,3). The ordinate of vertex C is
View SolutionLet ABC be a triangle. Let A be the point (1,2),y=x be the perpendicular bisector of AB, and x−2y+1=0 be the angle bisector of ∠C . If the equation of BC is given by ax+by−5=0 , then the value of a+b is (a)1(b) 2(c) 3 (d) 4
View SolutionConsider a triangle ABC with vertex A(2,−4). The internal bisectors of the angle B and C are x+y=2 andx−3y=6 respectively. Let the two bisectors meet at I.if (a, b) is incentre of the triangle ABC then (a+b) has the value equal to
View SolutionThe equations of the perpendicular bisectors of the sides AB&AC of a triangle ABC are x−y+5=0&x+2y=0. find the equation of the bc
View Solution
