Prove that the area of the parallelogram contained by the lines 4y−3x−a=0,3y−4x+a=0,4y−3x−3a=0, and 3y−4x+2a=0 is (27)a2.
Video Solution
Text Solution
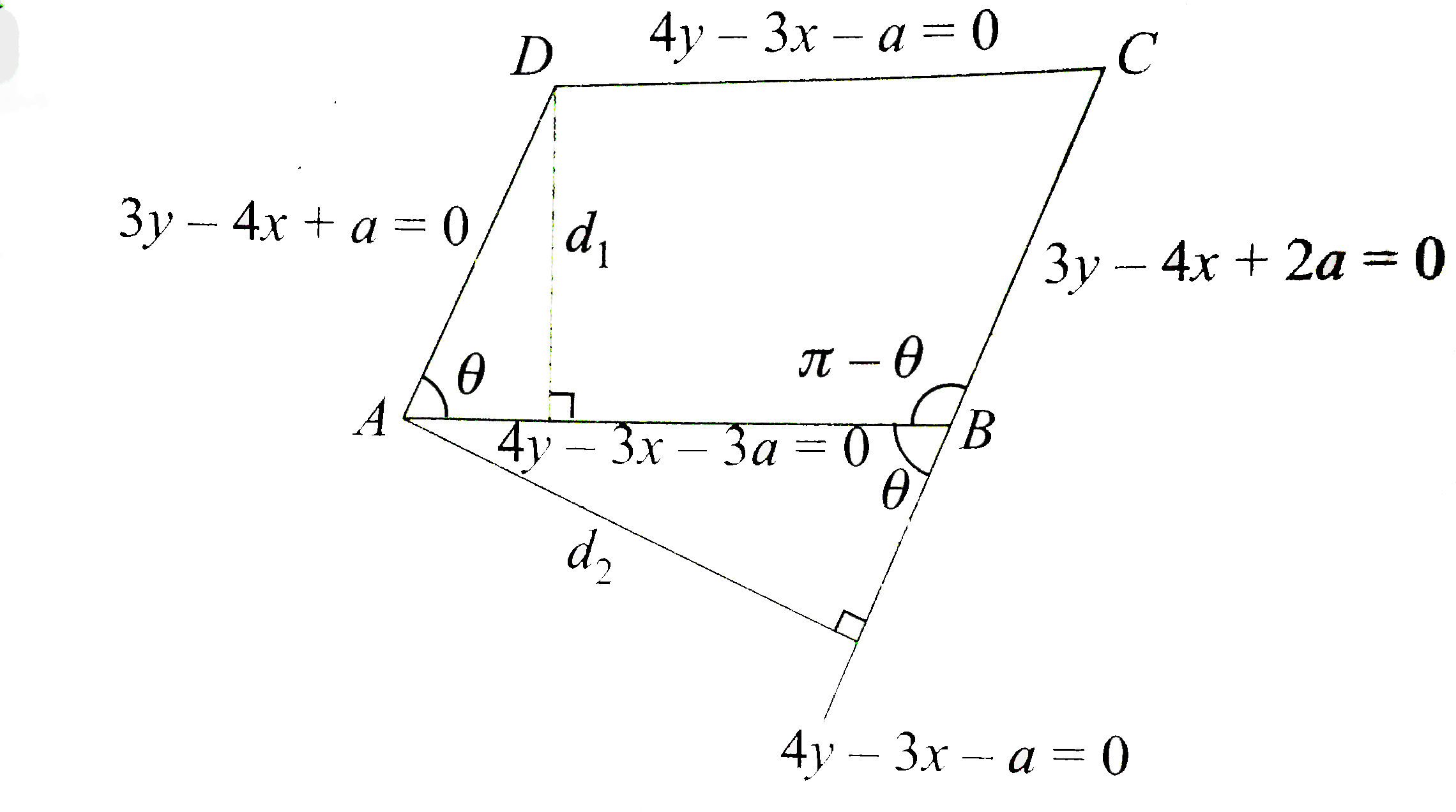
tanθ=∣∣∣(4/3)−(3/4)1+(4/3)×(3/4)∣∣∣=724
orcosecθ=257
Now d1=|−a+3a|5=∣2a5
and d2=|2a−a|5=∣∣∣a5∣∣∣
∴ Area=2(Area ofΔABD)=2(12d1⋅AB)
=d1d2cosec θ=(∣∣∣a5∣∣∣)(∣∣∣2a5∣∣∣)257=2a27
|
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Knowledge Check
The area of the parallelogram formed by the lines 2x−3y+a=0,3x−2y−a=0,2x−3y+3a=0 and 3x−2y−2a=0 in square units , is
Aa25B2a25C3a25Dnone of theseThe lines x+2y−5=0,2x−3y+4=0,6x+4y−13=0
Aare concurrentBform a right angled triangleCform an isosceles triangleDform an equilateral triangle.The perimeter of a parallelogram whose sides are represented by the lines x+2y+3=0,
3x+4y−5=0,2x+5=0and3x+4y−10=0 is equal toA52+5√5 unitsB5+4√5 unitsC5+52√5 unitsD5+5√52 units
Prove that the diagonals of the parallelogram formed by the four lines 3x+y=0,3y+x=0,3x+y=4,3y+x=4 are at right angles.
View SolutionThe area of the parallelogram formed by the lines 3x−4y+1=0,3x−4y+3=0,4x−3y−1=0 and 4x−3y−2=0, is (A) 17squnits (B) 27squnits (C) 37squnits (D) 47squnits
View SolutionFind the area of the parallelogram formed by the lines
2x2+5xy+3y2=0and2x2+5xy+3y2+3x+4y+1=0
View SolutionIf area of the parallelogram formed by the lines x+3y−a=0,3x−2y+3a=0,x+3y+4a=0 and 3x−2y+7a=0 is 220 sq. units, then value of a is ________
View SolutionFind the orthocenter of the triangle formed by the lines x+2y=0,4x+3y−5=0,3x+y=0.
View Solution
