Question

Consider a triangle with vertices ${\displaystyle A(1,2),B(3,1),}$
and ${\displaystyle C(-3,0)\stackrel{.}{}}$
Find
the equation of altitude through vertex ${\displaystyle A\stackrel{.}{}}$

the equation of median through vertex ${\displaystyle A\stackrel{.}{}}$

the equation of internal angle bisector of ${\displaystyle \angle A\stackrel{.}{}}$

Explanation

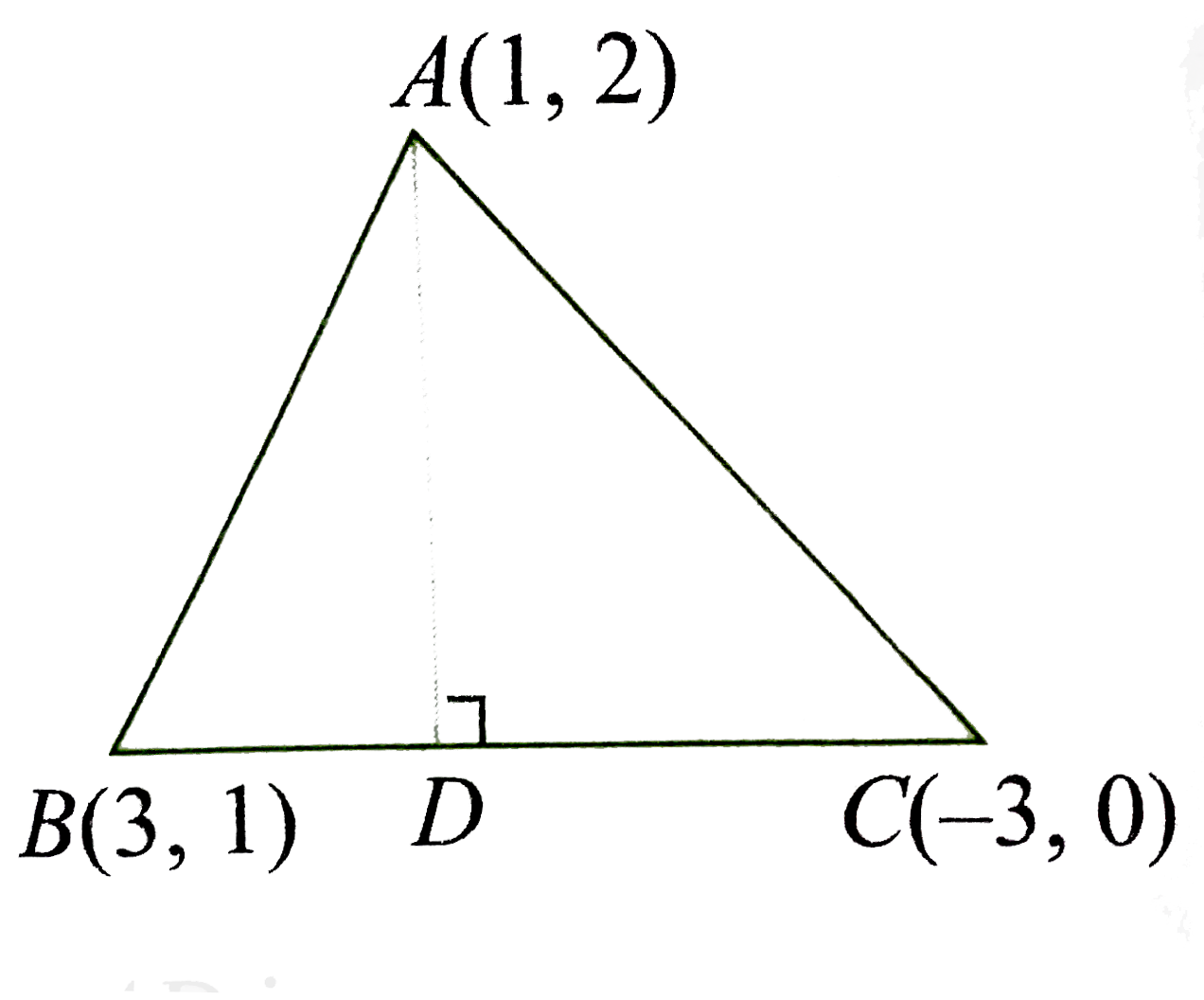
Let the altitude through A be AD.
Now, AD `bot` BC
Slope of BC `=(1-0)/(3-(-3)) = (1)/(6)`
therefore, the equation of altitude AD is
y-2 = -6(x-1)
or 6x + y - 8 = 0

(ii) The median through A passes through the midpoint of BC.
Now, the midpoint of BC is E(3-3)/2, (1+0)/2) or E(0,1/2).
Therefore, the equation of
median AE is `y-2 = (2-(1//2))/(1-0)(x-1)`
or 3x-2y+1 = 0

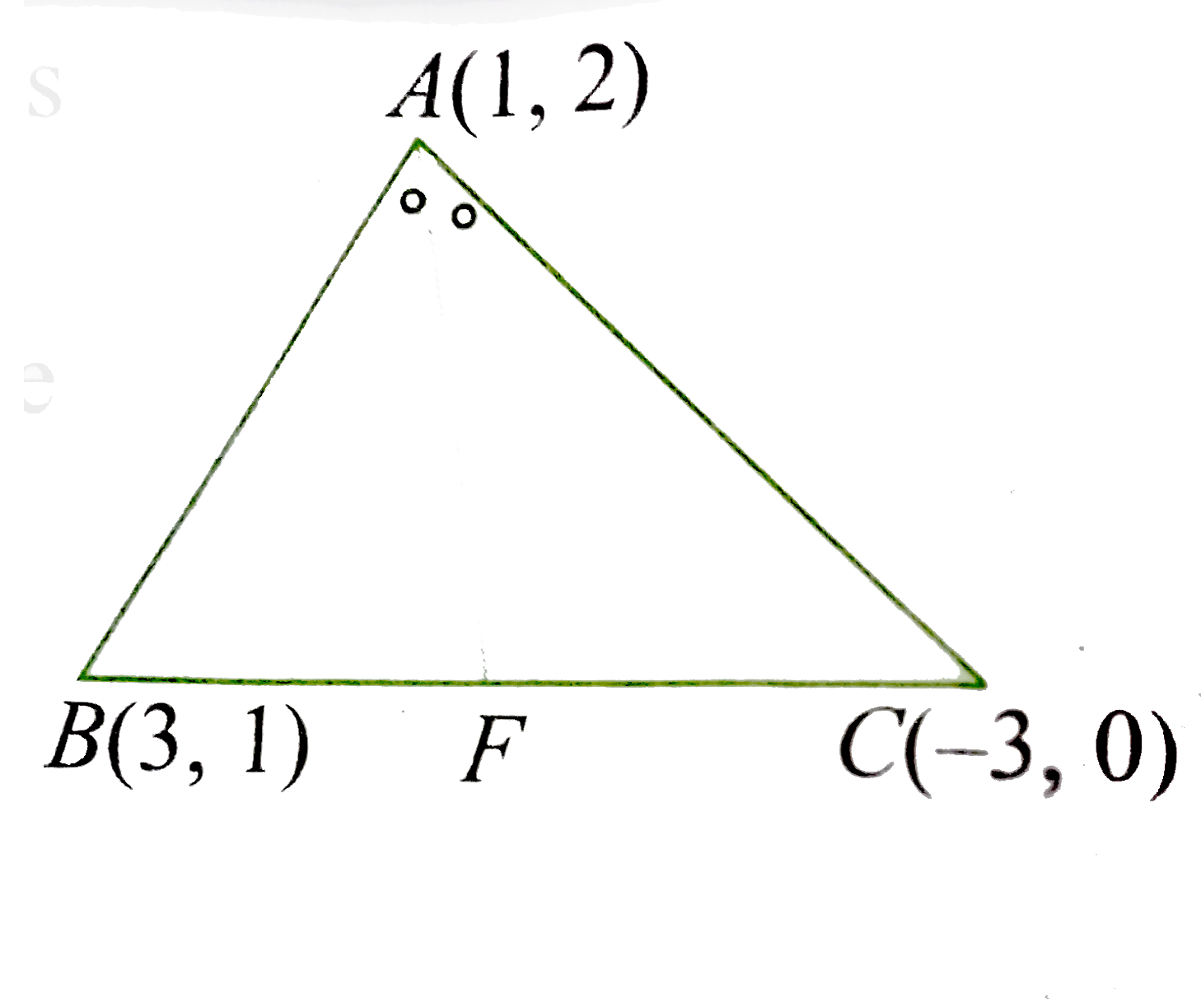
Let the internal bisector of A meets the side BC in F.
Now, the point F divides BC in the ratio
`("BF")/("CF") = ("AB")/("AC") = (sqrt(5))/(sqrt(20)) = (1)/(2)`
Therefore, the coordinates of F are
`((2(3) + 1(-3))/(2+1),(2(1) + 1(0))/(2+1)) = (1,(2)/(3))`
Therefore, the slope of AF is `oo`.
Hence, the equation of AF is x-1 = 0.