Question

If a continuous function $f$ defined on the real line R assume positive and negative values in R, then the equation $f\left(x\right)=0$ has a root in R. For example, if it is known that a continuous function $f$ on R is positive at some point and its minimum value is negative, then the equation $f\left(x\right)=0$ has a root in R. Consider $f\left(x\right)=k{e}^x-x$, for all real x where k is a real constant.
The line $y=x$ meets $y=k{e}^x$ for $k\le 0$ at

Options

A. `(1)/(e)`
B. 1
C. `e`
D. `log_(e)2`

Explanation

(a) `ke^(x)-x=0` to have only one positive root means the line `y=(x)/(k)` must be tangential to the curve `y=e^(x)`.

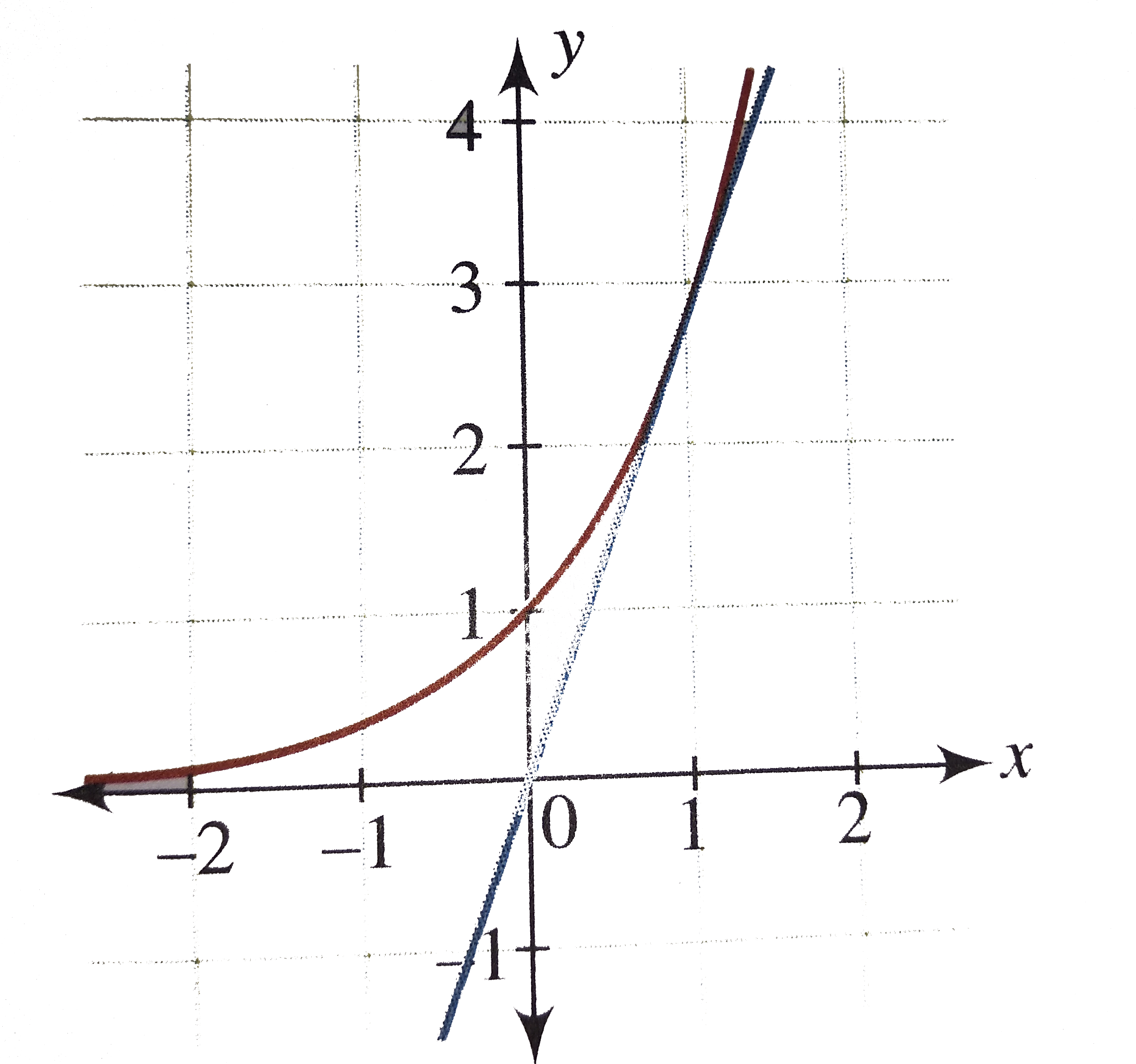
Let the line touch the curve at `(x_1, y_1)`, then
`" "((dy)/(dx))_(x_1)= e^(x_1)= (1)/(k)`
`" "` Also `y_1 = e^(x_1) and y_1 = (x-1)/(k)`
`" "rArr x_1 =1 rArr k= 1//e`