Three particle each of mass $m$ , are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?

Video Solution

Text Solution

Verified by Experts

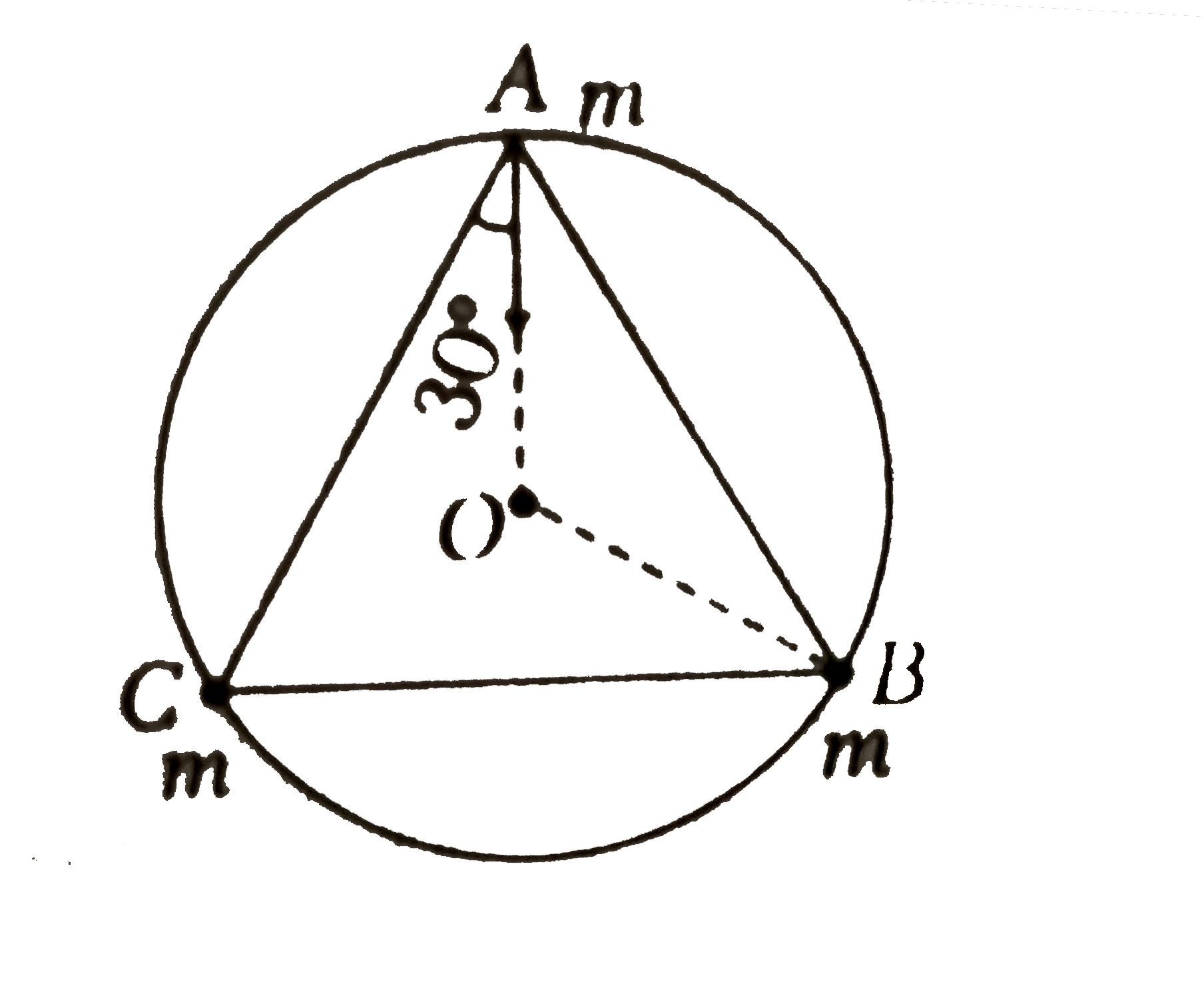
Let $A, B$ and $C$ be the three masses and $O$ the centre of the circumscribing circle The radius of this circle is
$R = \frac{L}{2} sec 30^{\circ} = \frac{L}{2} \times \frac{2}{\sqrt{3}} = \frac{L}{\sqrt{3}}$
let v be the speed of each mass $M$ along the circle Let us consider the motion of the mass at A The force of gravitational attraction on it due to the masses at $B$ and $C$ are
$\frac{G M^{2}}{L^{2}}$ along AB and $\frac{G M^{2}}{L^{2}}$ along AC
The resultant force is therefore
$2 \frac{G M^{2}}{L^{2}} {cos 30}^{\circ} = \frac{\sqrt{3} G M^{2}}{L^{2}} a l o n g A D$
This for preserving the triangle must be equal to the neceassary centripetal force That is
$\frac{\sqrt{3} G M^{2}}{L^{2}} = \frac{M v^{2}}{R} = \frac{\sqrt{3} M v^{2}}{L} [∵ R = L / \sqrt{3}]$ or $v = \frac{\sqrt{G M}}{L}$
.

Updated on:21/07/2023

Three particles each of mass $m$ are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
Azero
B $\frac{3 G M}{L^{2}}$
C $\frac{9 G M}{L^{2}}$
D $\frac{12 G M}{\sqrt{3} L^{2}}$
Three indentical bodes of mass M are locatd at the verticles of an equailateral triangle of side L they revolve undr the effect of mutual gravitational force in a circular orbit circumscibing the traingle while preserving the equilateral triangle their orbital velocity is
A $\frac{\sqrt{G M}}{L}$
B $\sqrt{3 G M} / (2 L)$
C $\frac{\sqrt{3 G M}}{L}$
D $\frac{\sqrt{2 G M}}{3 L}$
Three particles each of mass $m$ are kept at the vertices of an euilateral triangle of side $L$ . The gravitational field at the centre due to these particle is
A $- \frac{3 G M}{L}$
B $- \frac{\sqrt{3} G M}{L}$
C $- \frac{3 \sqrt{3} G M}{L}$
D $- \frac{G M}{3 \sqrt{3} L}$