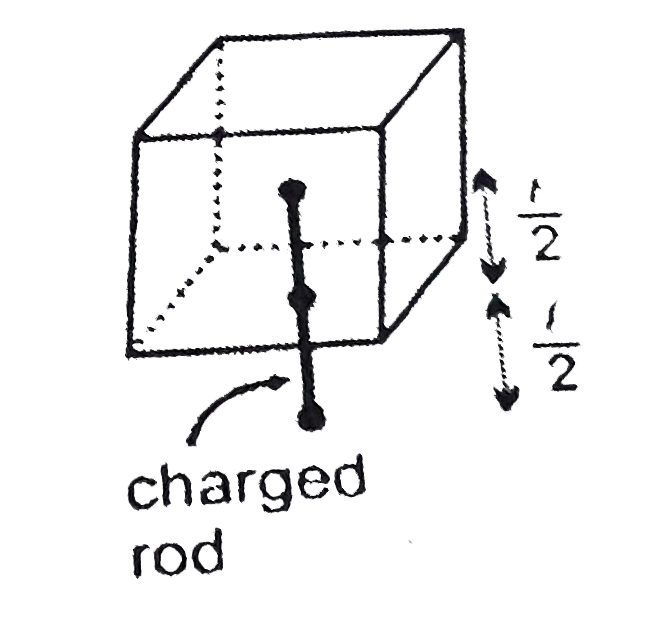
A charge Q is uniformly distributed over a rod of length $l$ . Consider a hypothetical cube of edge $l$ with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.

Video Solution

Text Solution

Verified by Experts

According to Gauss law : Flux depends upon charge inside the closed hypothetical surface. So for minimum possible flux through the entire surface of the cube, charge inside it should be minimum.
Linear charge density of rod $= \frac{Q}{l}$
and minimum length of rod inside the cube $= \frac{l}{2}$
So, charge inside the cube $= \frac{l}{2} . \frac{Q}{l} = \frac{Q}{2}$
So, fluc through the entire surface of the cube $= \frac{Σ q}{\in_{0}} = \frac{Q}{2 \in_{0}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Charge Q is uniformly distributed on a dielectric rod AB of length $2 l$ . The potential at P shown in the figure is equal to

A $\frac{Q}{4 π ε_{0} (2 l)}$
B $\frac{Q}{4 π ε_{0} (l)} ln 2$
C $\frac{Q}{4 π ε_{0} (2 l)} ln 3$
DNone of these
Question 2 - Select One
A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is

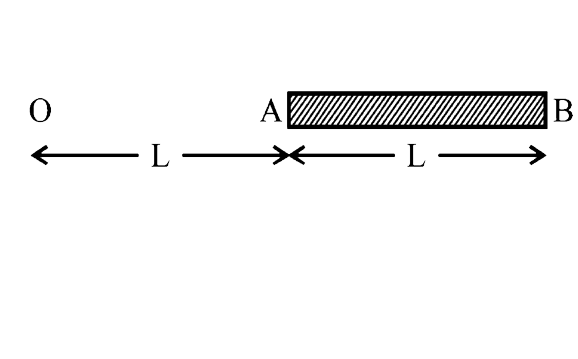A(a) $\frac{Q}{8 π ε_{0} L}$
B(b) $\frac{3 Q}{4 π ε_{0} L}$
C(c) $\frac{Q}{4 π ε_{0} L 1 n 2}$
D(d) $\frac{Q 1 n 2}{4 π ε_{0} L} s$
Question 3 - Select One
A long string with a charge of a per unit length passes through an imaginary cube of edge L. The maximum possible flux of electric field through the cube will be
A $\frac{λ L}{ε_{0}}$
B $\frac{\sqrt{2} λ L}{ε_{0}}$
C $\frac{\sqrt{3} λ L}{ε_{0}}$
D $\frac{\sqrt{5} λ L}{ε_{0}}$

RESONANCE-ELECTROSTATICS-Problems

Home
Ask Doubt
Profile