A rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induced in the rod at the instant shown in .
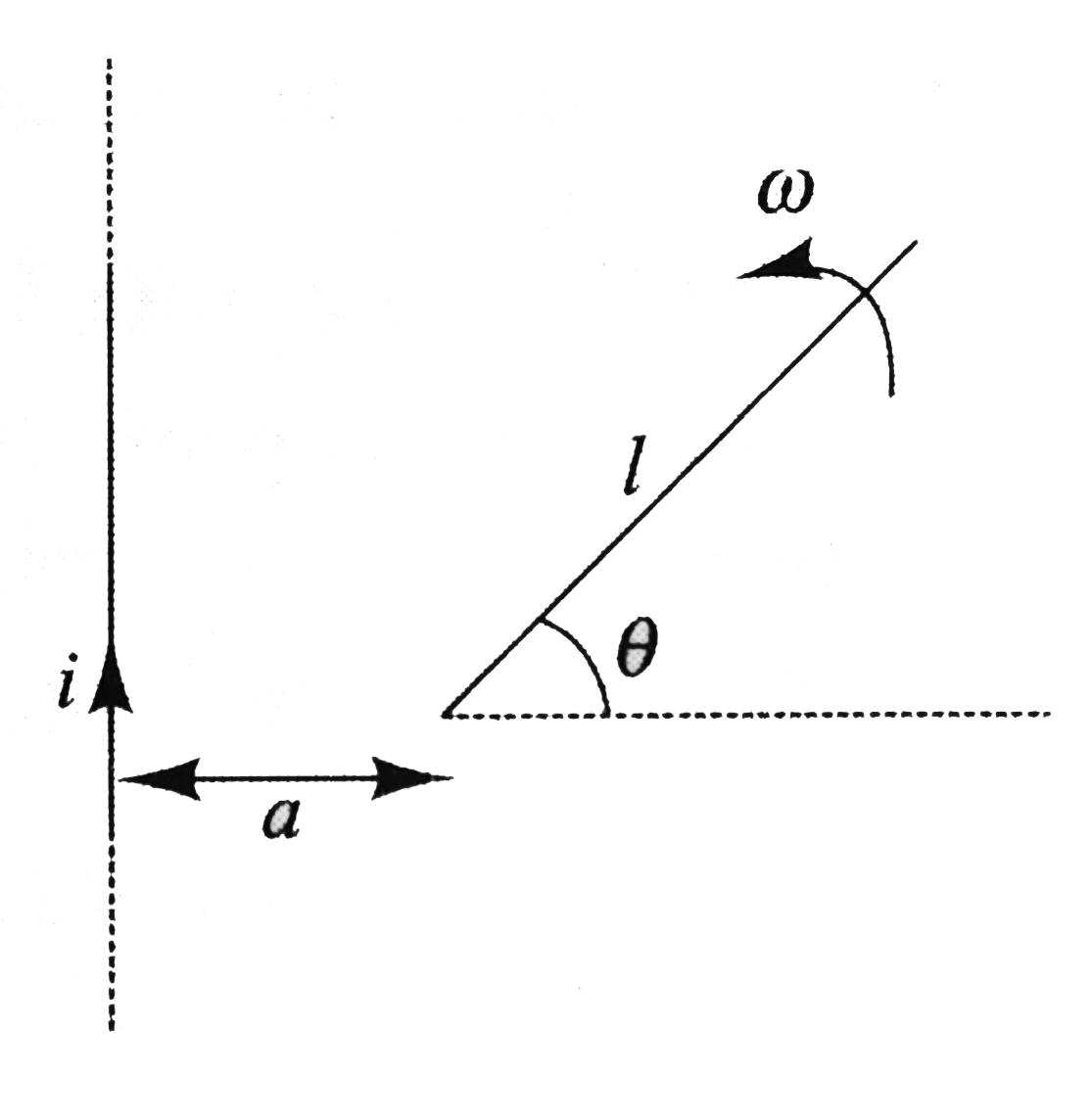
E=∫μ0i2π(a+rcosθ)×(rω)⋅(dr)
E=μ0ωi2π∫l0ra+rcosθdr⇒E=μ0Iω2πcosθ[l−acosθln(a+lcosθa)]
Similar Questions
A rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induecd in the rod at the instanr shown in .
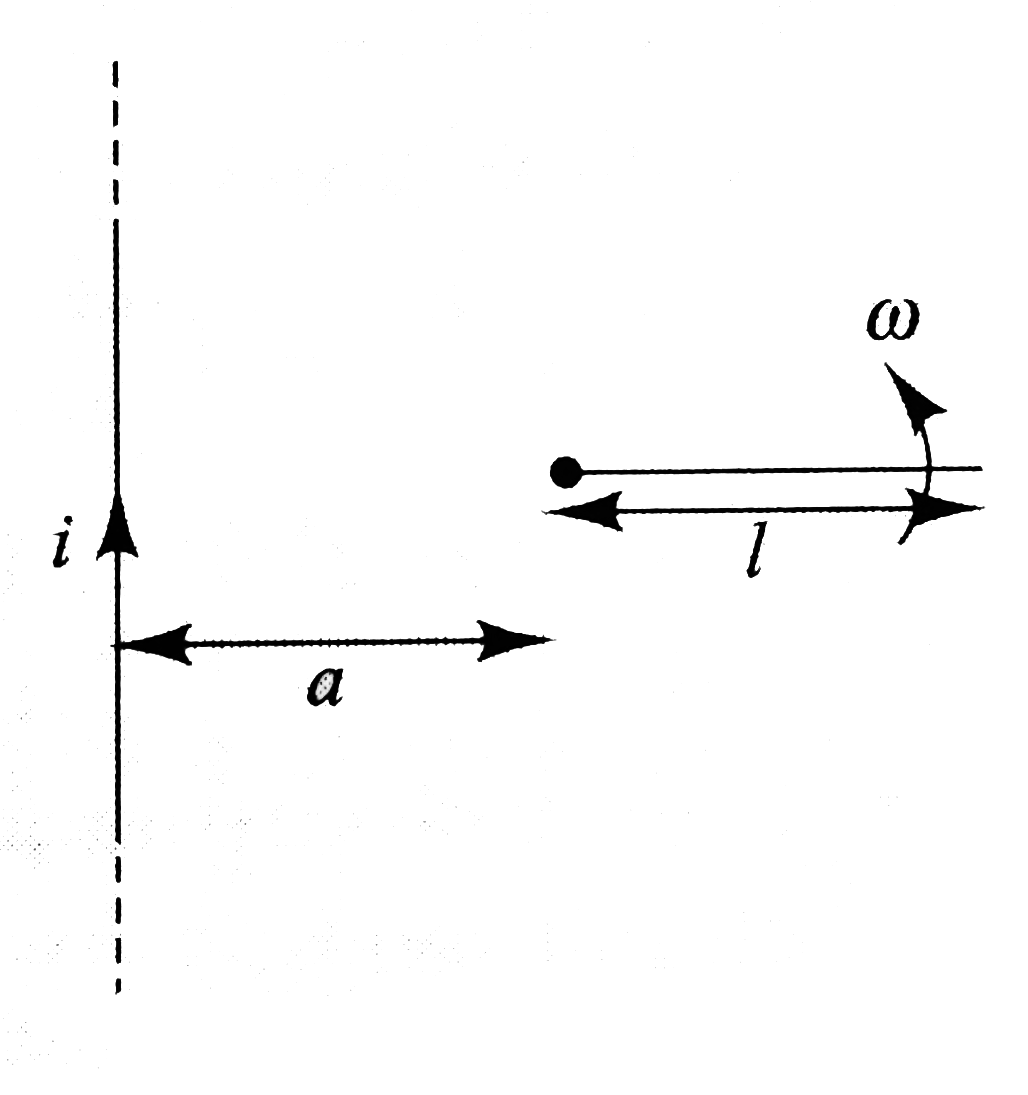
View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.

View Solution
Knowledge Check
A conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
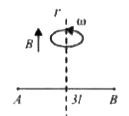 A12Bωl2B18Bωl2CZeroDBωl2
A12Bωl2B18Bωl2CZeroDBωl2A conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
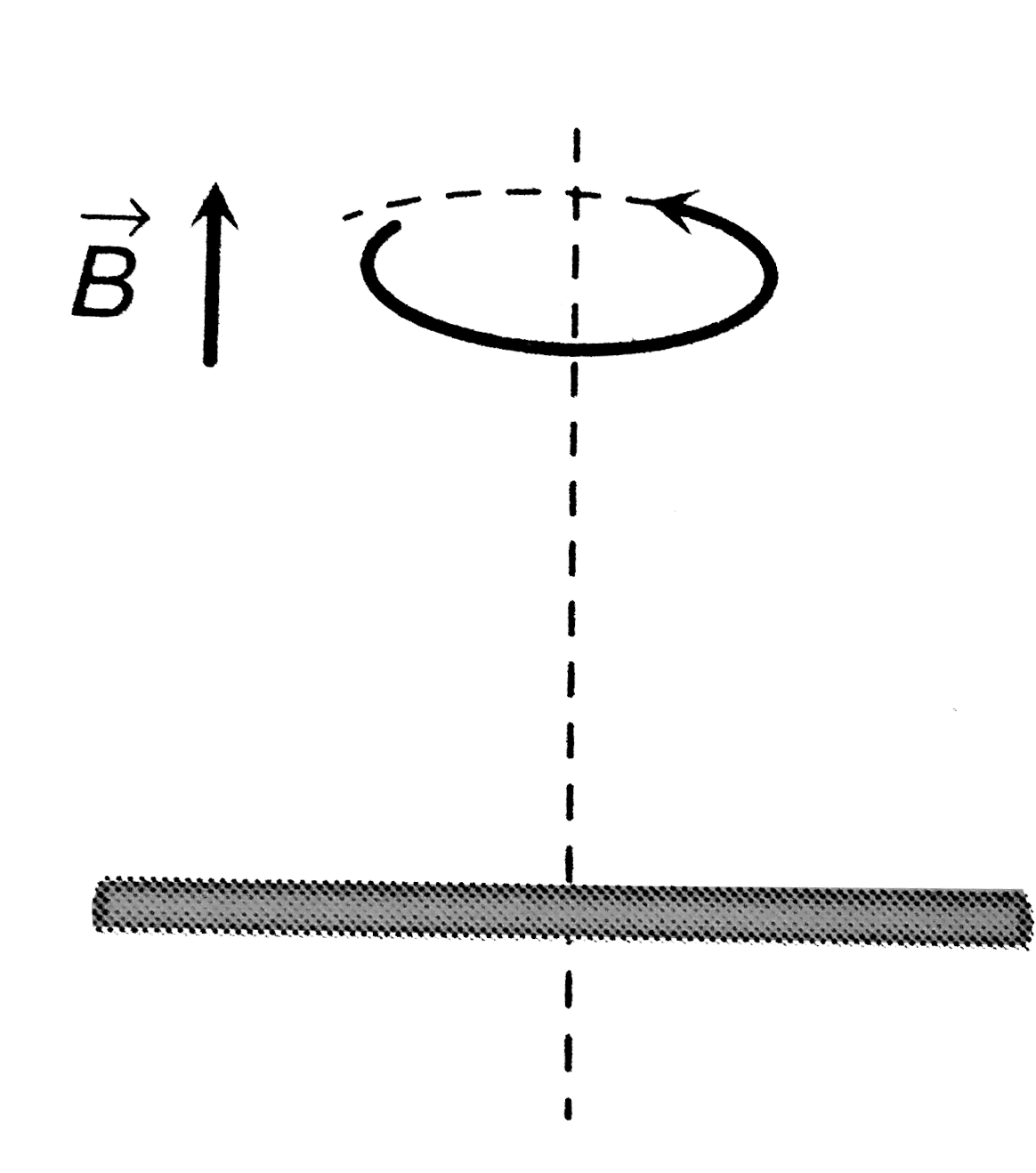 ABωl2B12Bωl2C18Bωl2Dzero
ABωl2B12Bωl2C18Bωl2DzeroIn the figure shown AB is a plastic rod moving with a constant velocity v, W is an infinite long wire carrying current I. The end of the rod which is at higher potential is
 AABBCNo emf will br induced in the rodDNone of the above
AABBCNo emf will br induced in the rodDNone of the above
a rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png)
View Solution
