Shows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
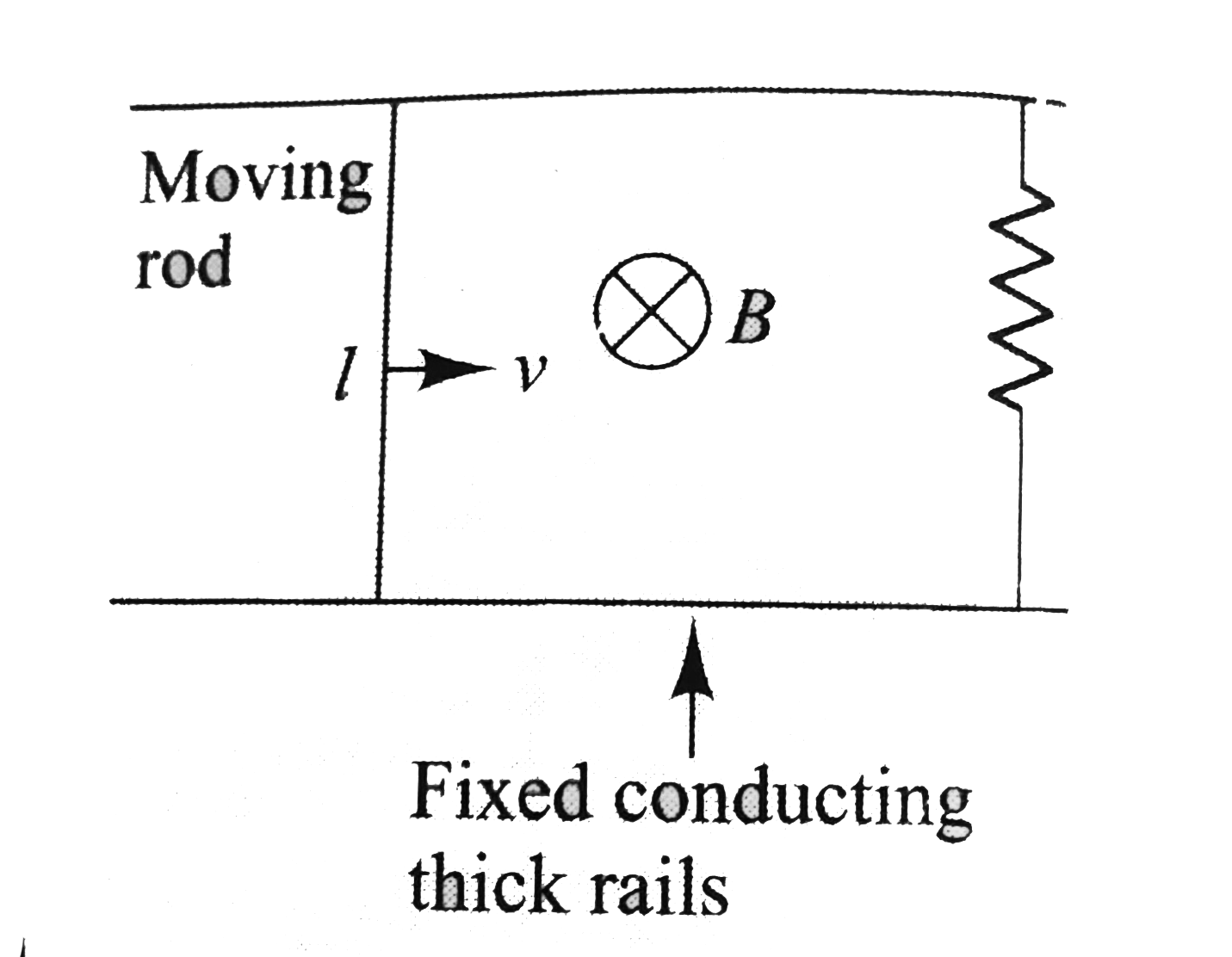
Similar Questions
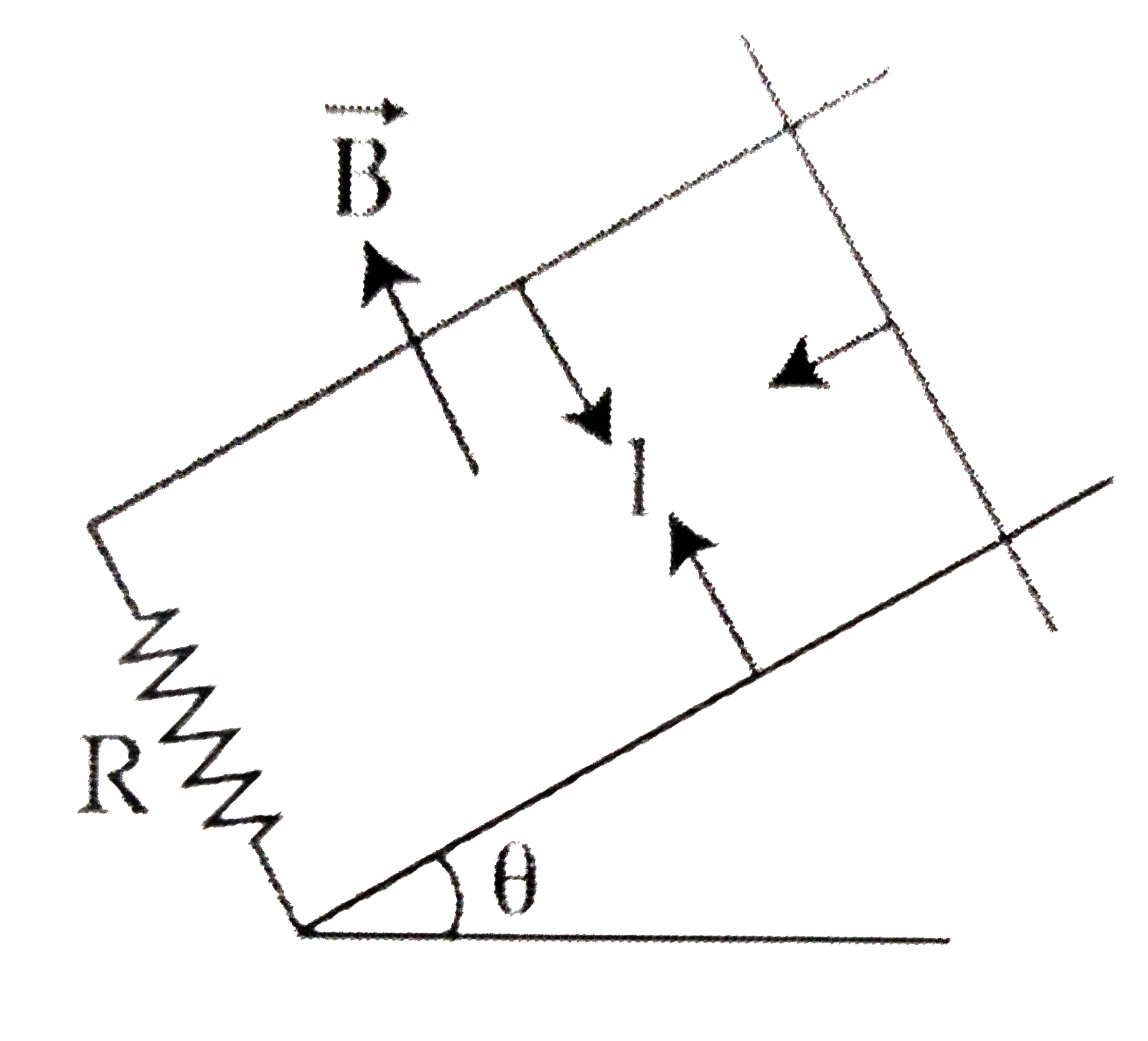
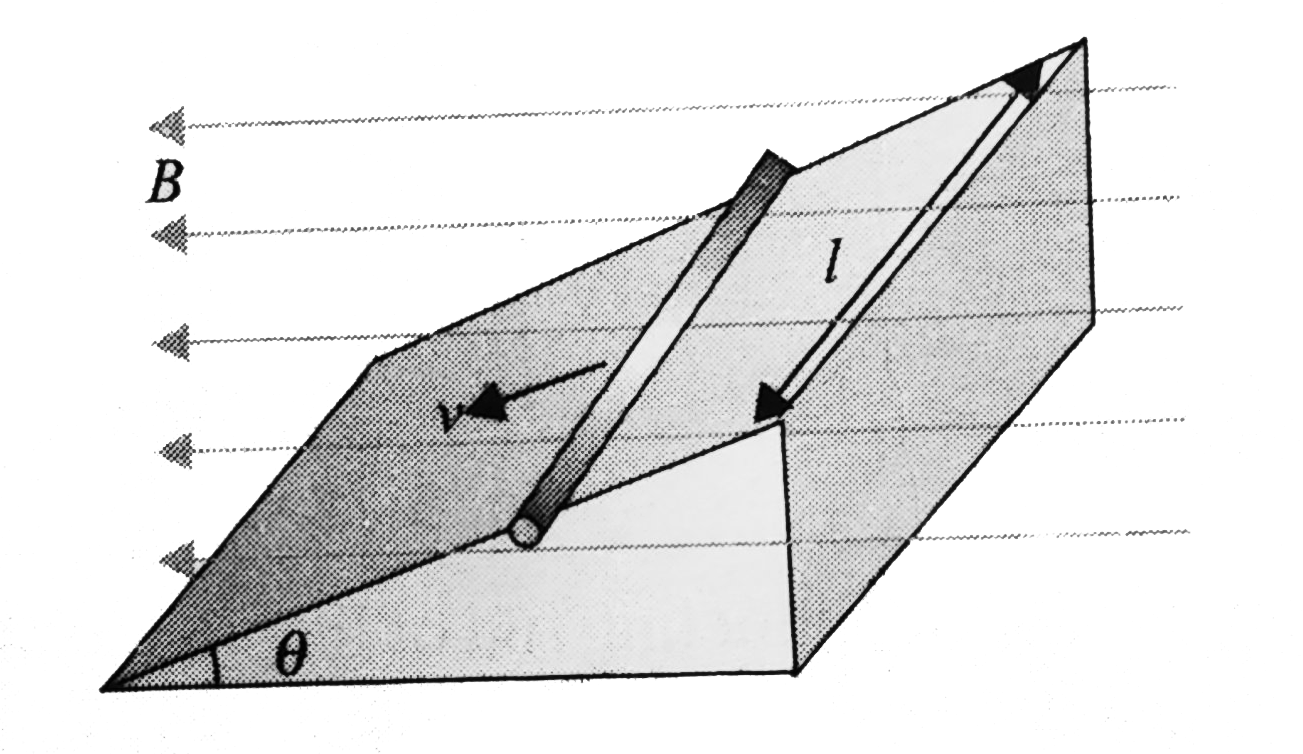
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
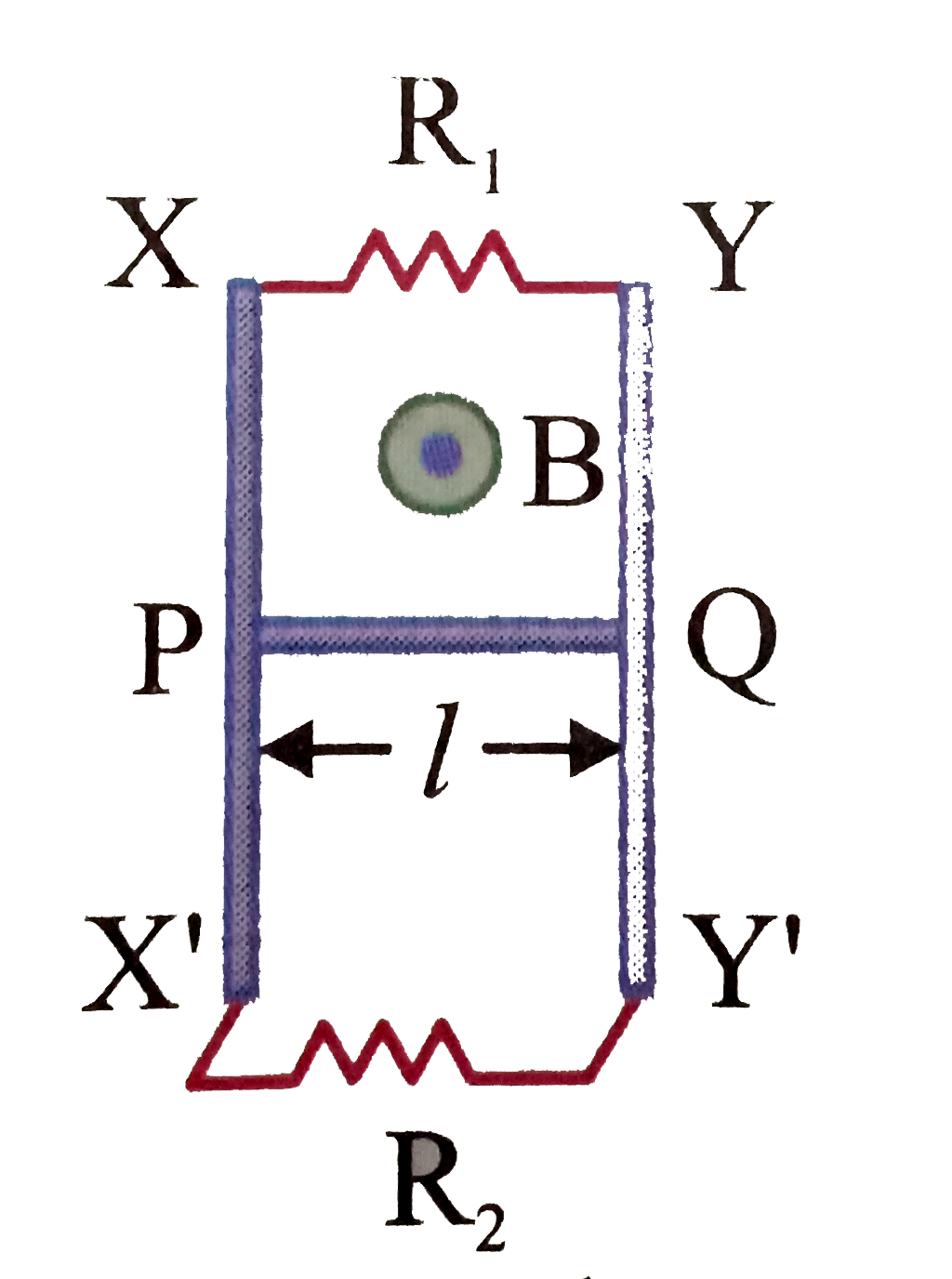
View SolutionTwo parallel vertical metallic bars XX1 and YY1, of negligible resistance and separated by a length 'l', are as shown in Fig. The ends of the bars are joined by resistance R1 and R2. A uniform magnetic field of induction B exsits in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is oberved that in the steady state the powers dissipated in the resistance R1 and R2 and the terminal velocity attained by the rod PQ.
View Solution
Knowledge Check
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.
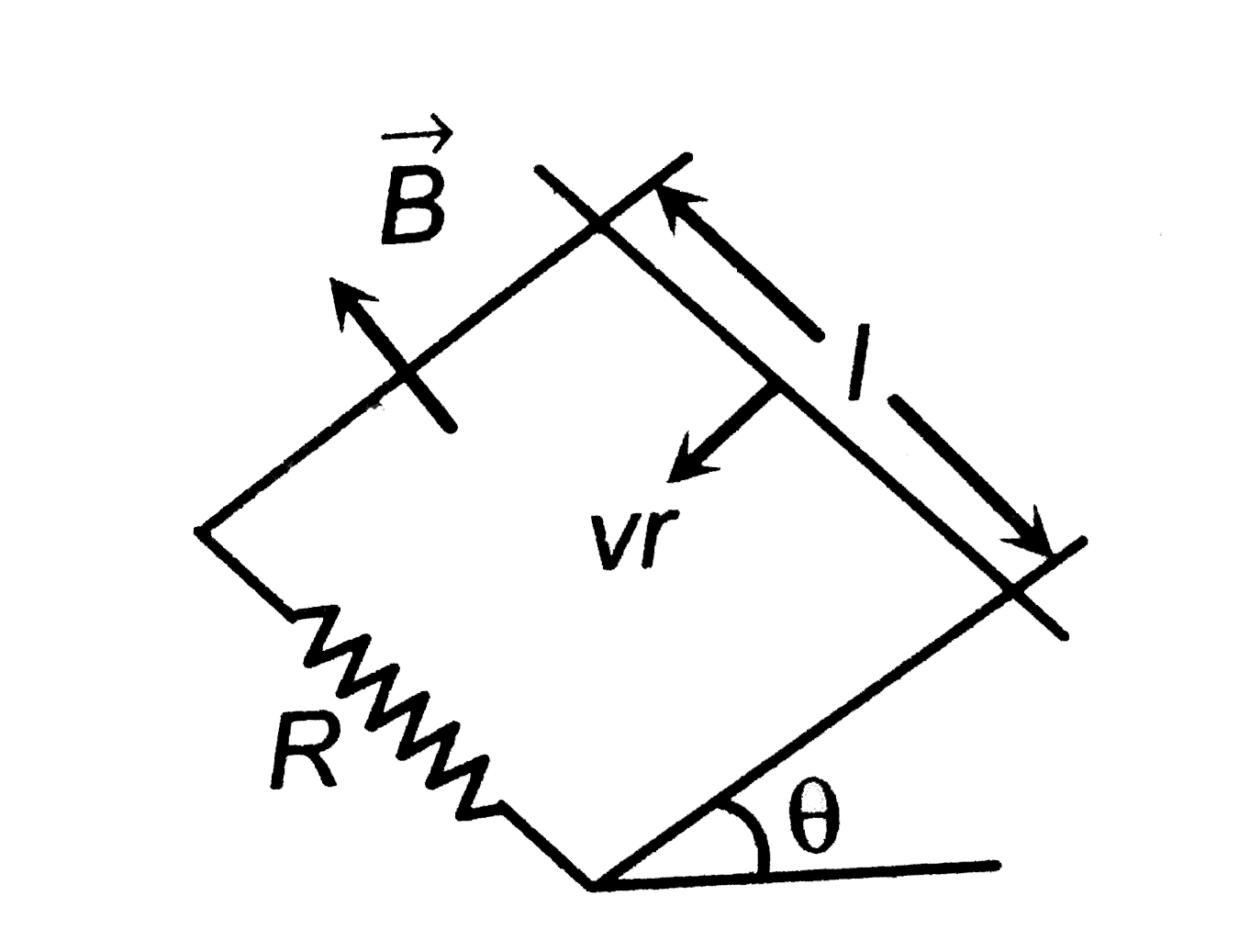
There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRcosθB2l2BmgRsinθB2l2CmgRtanθB2l2DmgRcotθB2l2A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRtanθB2l2BmgRcotθB2l2CmgRsinθB2l2DmgRcosθB2l2A conducting rod of mass m and length l is free to move without friction on two parallel long conducting rails, as shown below. There is a resistance R across the rails. In the entire space around, there is a uniform magnetic field B normal to the plane of the rod and rails. The rod is given an impulsive velocity v0-

Finally, the initial energy 12mv20AWill be converted fully into heat energy in the resistorBWill enable rod to continue to move with velocity v0 since the rails are frictionlessCWill be converted fully into magnetic energy due to induced currentDWill be converted into the work done against the magnetic field
A rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
View SolutionA conducting rod of length l slides at constant velocity v on two parallel conducting rails, placed in a uniform and constant magnetic field B perpendicular to the plane of the rails as shown in Fig.3.49. A resistance R is connected between the two ends of the rails.

(a) Idenify the cause which produces change in magnetic flux.
(b) Identify the direction of current in the loop.
( c) Determine the emf induced in the loop.
(d) Compute the electric power dissipated in the resistor.
(e) Calcualte the mechenical power required to pull the rod at a cinstant velovity.
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionTwo parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are λ no other wire has resistance. Then :

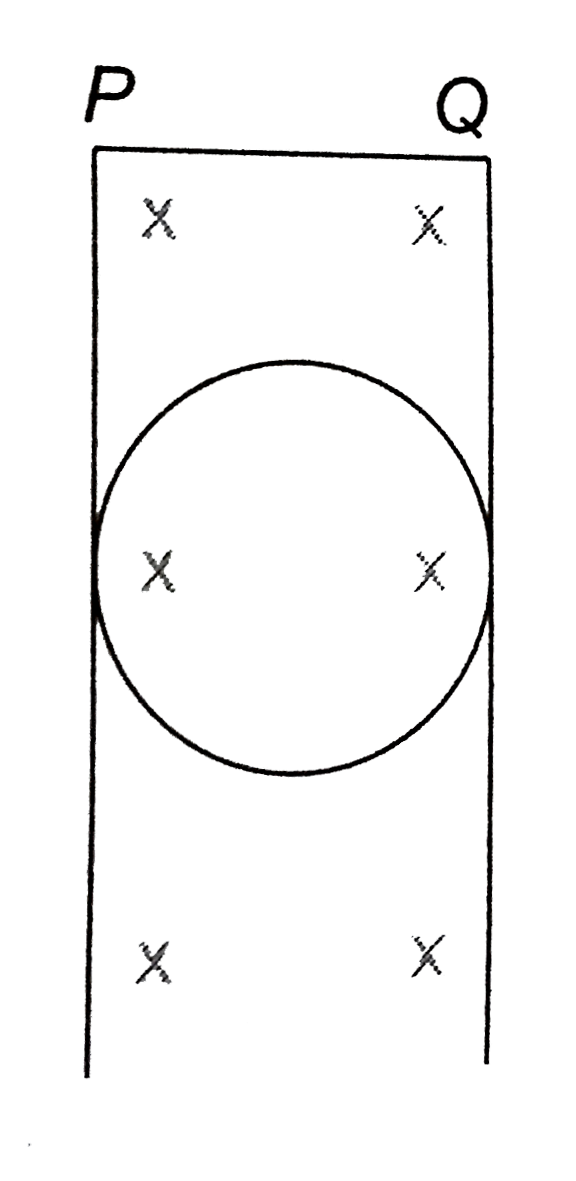
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
View Solution

