(i) Find whether f(x)=x+cosx is one-one.
(ii) Identify whether the function f(x)=−x3+3x2−2x+4 for f:R→R is ONTO or INTO
(iii) f(x)=x2−2x,[0,3]→A. Find whether f(x) is injective or not. Also find the set A if f(x) is surjective
Video Solution
Text Solution
(i) The domain of f(x) is R . f'(x)=1−sinx
∴F'(x)≥0∀xε complete domain and equality holds at discrete points only
∴f(x) is strictly increasing on R. Hence f(x) is one-one.
(ii) As range ≡ codomain, therefore given function is ONTO
(iii) f'(x)=2(x−1),0≤x≤3
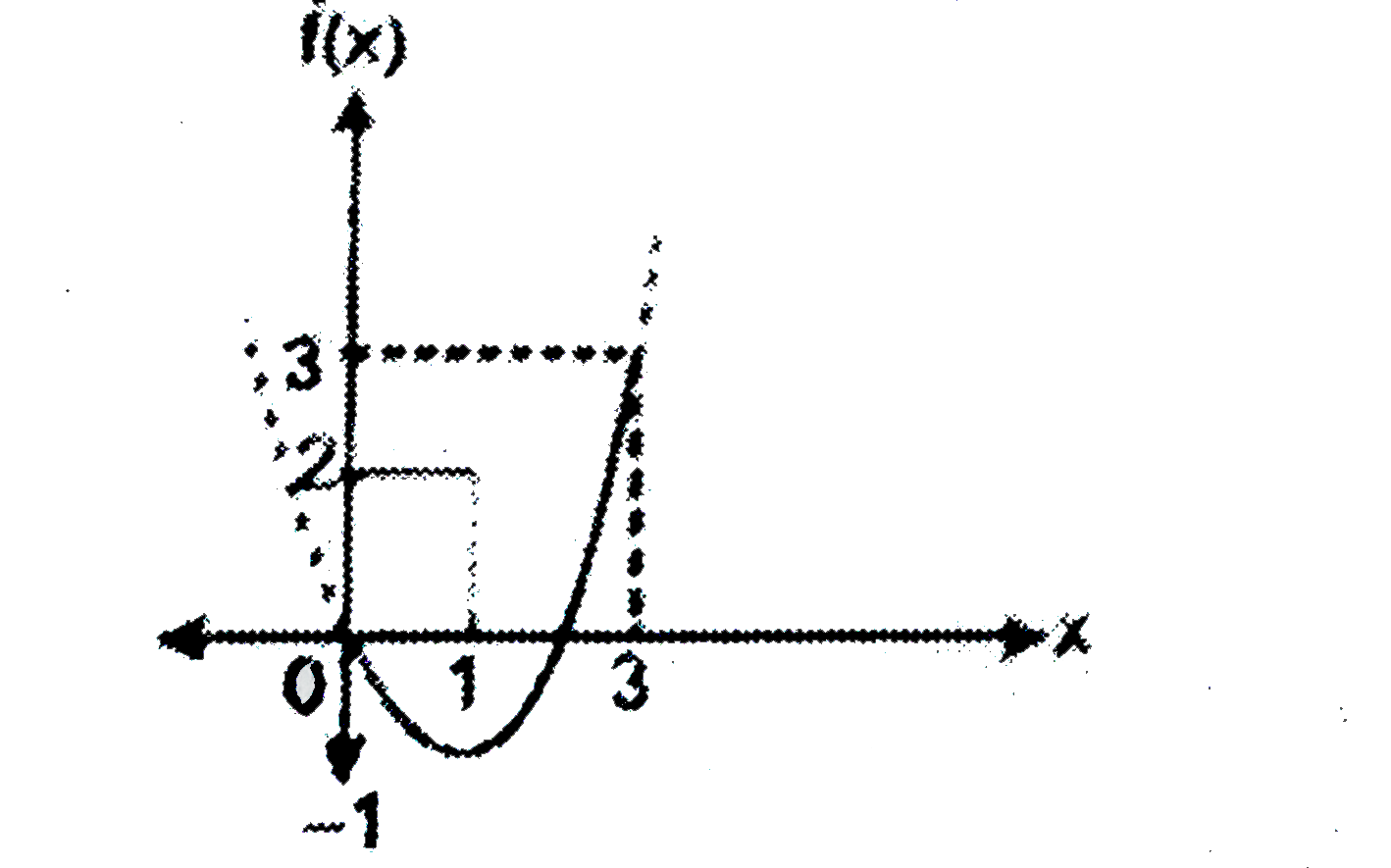
∴f'(x)={−ve0≤x<1+ve1<x<3
∴f(x) is non monotonic. Hence it is not injective.
For f(x) to be surjective, A should be equal to its range. By graph range is [−1,3]
∴A≡[−1,3]
|
Topper's Solved these Questions
- RELATION, FUNCTION & ITFBOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - SUBJECTIVE_TYPE
180 Videos
- RELATION, FUNCTION & ITFBOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN
5 Videos
- NUMBER THEORYBOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4 Videos
- SEQUENCE & SERIES BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3 Videos
Similar Questions
f(x)=x2−2x+3,[0,3]→A. Find whether f(x) is injective or not. Also find the set A, if f(x) is surjective.
View SolutionFind whether f(x)=x+cosx is one-one.Identify whether the function f(x)=−x3+3x2−2x+4 for f:R→R is ONTO or INTO
View Solutionfind f(4) if f(x)=x2+2x−3
View SolutionShow that the function f(x)=3x+2 is one-one and onto
View SolutionFind whether f(x) is one-one or many-one & into or onto if f:D->R where D is its domain. f(x)=34x2−cosπx
View SolutionIf f(x)=x3+2x, then find the value of f(3).
View SolutionIf f(x)=x3+3x2−2x+4, find f(−2)+f(2)−f(0).
View SolutionIf f(x)=x2+2x+7 , find f ' (3) .
View SolutionIf f(x)={x2x≠0,4x=0 then find whether f(x) is continuous at x=0
View SolutionLet f:[−π/2,π/2]→[−1,1] where f(x)=sinx. Find whether f(x) is one-one or not.
View Solution
