Estimate the value of $\int_{0}^{a} e^{x^{2}} d x$ using (i) rectangle, (ii) triangle.

Video Solution

Text Solution

Verified by Experts

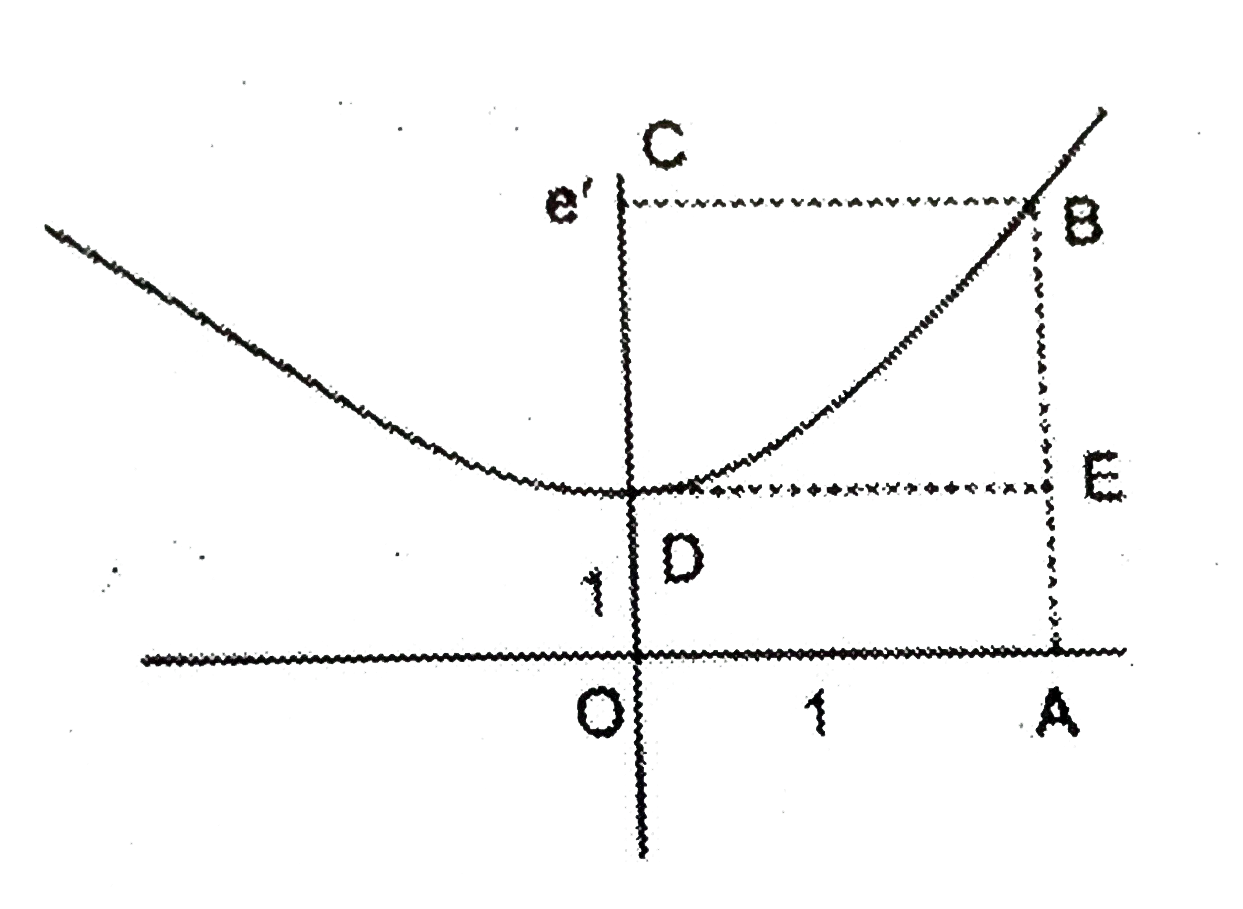
By using rectangle
Area $O A E D < 1 \int 0 e^{x^{2}} d x <$ Area OABC
$1 < 1 \int 0 e^{x^{2}} d x < e$
(ii) By using triangle
Area $O A E D < 1 \int 0 e^{x^{2}} d x <$ Area $O A E D +$ Area of triangle $D E B$
$1 < {1 e 0}^{x^{2}} \int d x < 1 + \frac{1}{2.1} . (e - 1), 1 < 1 \int 0 e^{x^{2}} d x < \frac{e + 1}{2}$

Updated on:21/07/2023