A balloon is observed simultaneously from three points A, B and C on a straight road directly under it. The angular elevation at $B$ is twice and at $C$ is thrice that at $A$ . If the distance between A and B is 200 metres and the distance between B and C is 100 metres, then find the height of balloon above the road.

Video Solution

Text Solution

Verified by Experts

Let P be the balloon at height h above the road .

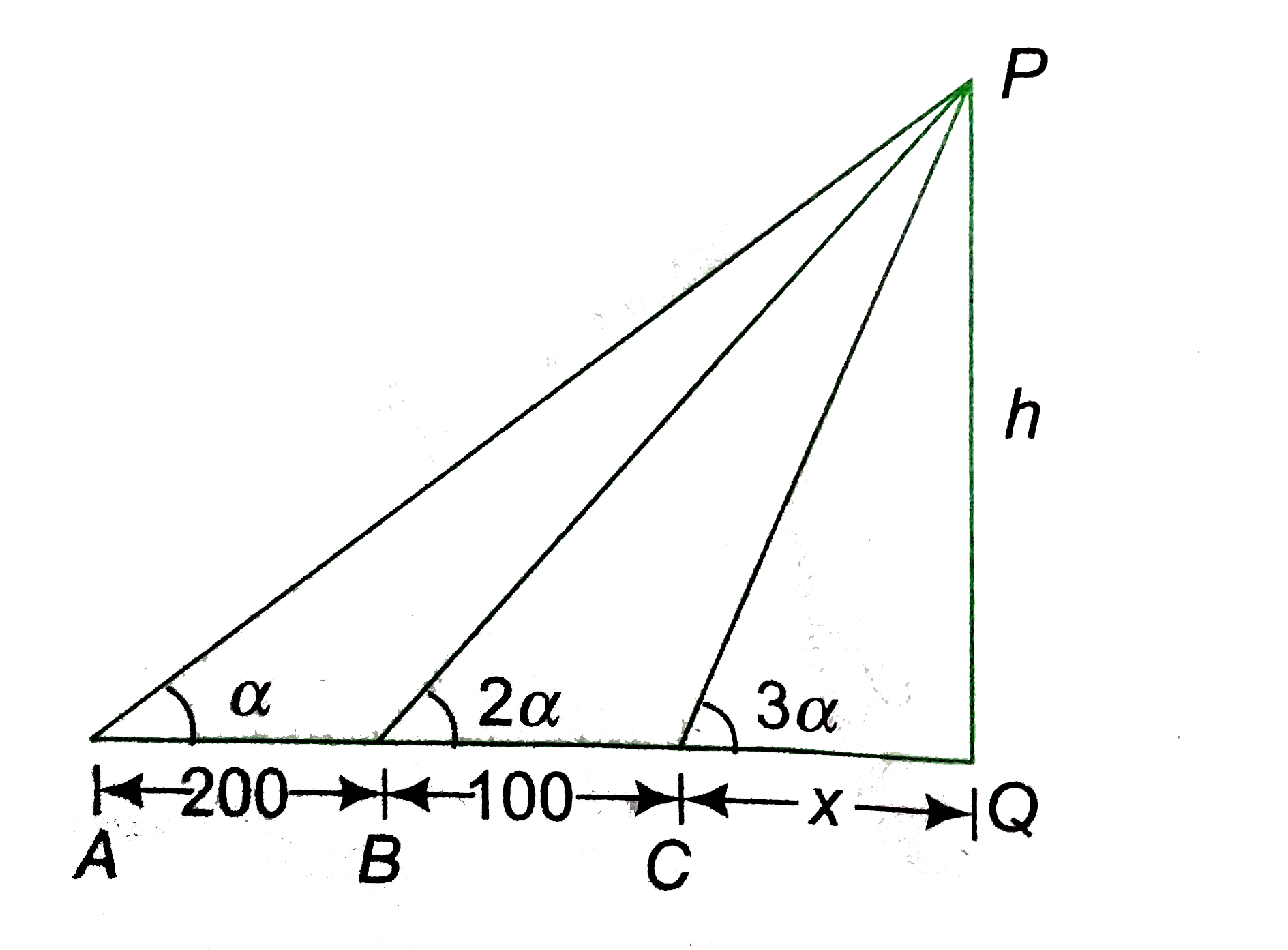
From the above figure ,
$x = h cot 3 α ... (1) < b r > (x + 100) = h cot 2 α ... (2) < b r > (x + 300) = h cot α \dots (3)$
Subtracting (1) from (2) ,we get
100=h(cot2alpha-cot3alpha) ,
$∴ 100 = h (\frac{sin α}{sin 3 α sin 2 α})$ ...(4) subtracting (2)from(3) , we get
$200 = h (cot α - cot 2 α)$
$∴ 200 = h (\frac{sin α}{sin 2 α sin α})$ ...(5)
Dividing (5) by (4), we get
$\frac{sin 3 α}{sin α} = \frac{200}{100} = 2$
rArr $3 sin α - 4 {sin}^{3} α - 2 sin α = 0$
$\Rightarrow {sin}^{2} α = \frac{1}{4} = {sin}^{2} \frac{π}{6}$
$\Rightarrow α = \frac{π}{6}$
using the value in (5) , we get
$∴ h = 200 sin \frac{π}{3} = 200 \frac{\sqrt{3}}{2} = 100 \sqrt{3}$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object is observed from the points A, B and C lying in a horizontal straight line which passes directly underneath the object. The angular elevation at B is twice that at A and at C three times that at A. If AB=a, BC=b, then the height of the object is
A $\frac{3 a}{2 b} \sqrt{(a + b) (3 b - a)}$
B $\frac{3 b}{2 a} \sqrt{(a + b) (3 a - b)}$
C $\frac{a}{2 b} \sqrt{(a + b) (3 b - a)}$
DNone of the above
Question 2 - Select One
An object is observed from the points A, B and C lying in a horizontal straight line which passes directly underneath the object. The angular elevation at B is twice that at A and at C three times that at A. If $A B = a, B C b$ then the height of the object is
A $\frac{3 a}{2 b} \sqrt{(a + b) (3 b - a)}$
B $\frac{3}{2 b} \sqrt{(a + b) (3 a - b)}$
C $\frac{a}{2 b} \sqrt{(a + b) (3 b - a)}$
DNone of these

CENGAGE-HIGHT AND DISTANCE -JEE Previous Year

Home
Ask Doubt
Profile