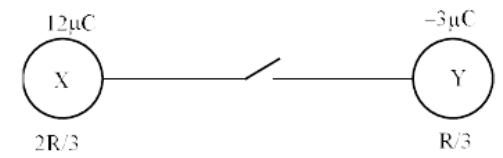
Two isolated conducting spheres $S_{1} and S_{2}$ of radius $\frac{2}{3} R and \frac{1}{3} R$ have $12 μ C$ and $- 3 μ C$ charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire . A long time after this is done the charges on $S_{1} and S_{2}$ are respectively :

A

$6 μ C and 3 μ C$

B

$4.5 μ C$ on both

C

$+ 4.5 μ C and - 4.5 μ C$

D

$1 μ C and 6 μ C$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to determine the final charges on the two conducting spheres $S_{1}$ and $S_{2}$ after they are connected by a conducting wire. Here are the steps to find the solution:
Step 1: Calculate the initial total charge
The initial charges on the spheres are:
- Charge on $S_{1}$ ( $Q_{1}$ ) = $12 μ C$
- Charge on $S_{2}$ ( $Q_{2}$ ) = $- 3 μ C$
The total initial charge $Q_{i n i t i a l}$ is given by:
$Q_{i n i t i a l} = Q_{1} + Q_{2} = 12 μ C + (- 3 μ C) = 12 μ C - 3 μ C = 9 μ C$
Step 2: Understand the concept of potential
When the two spheres are connected by a conducting wire, charge will flow between them until they reach the same electric potential. The potential $V$ of a conducting sphere is given by:
$V = \frac{k \cdot Q}{R}$
where $k$ is Coulomb's constant, $Q$ is the charge on the sphere, and $R$ is the radius of the sphere.
Step 3: Set up the equations for final charges
Let $Q_{f}$ be the final charge on $S_{1}$ and $Q_{f}^{'}$ be the final charge on $S_{2}$ . Since charge is conserved:
$Q_{f} + Q_{f}^{'} = Q_{i n i t i a l} = 9 μ C$
The radii of the spheres are:
- Radius of $S_{1}$ = $\frac{2}{3} R$
- Radius of $S_{2}$ = $\frac{1}{3} R$
The potentials of the spheres after they are connected must be equal:
$\frac{k \cdot Q_{f}}{\frac{2}{3} R} = \frac{k \cdot Q_{f}^{'}}{\frac{1}{3} R}$
Step 4: Simplify the potential equation
Canceling $k$ and $R$ from both sides gives:
$\frac{Q_{f}}{\frac{2}{3}} = \frac{Q_{f}^{'}}{\frac{1}{3}}$
This simplifies to:
$3 Q_{f} = 2 Q_{f}^{'}$
Step 5: Solve the equations
Now we have two equations:
1. $Q_{f} + Q_{f}^{'} = 9$
2. $3 Q_{f} = 2 Q_{f}^{'}$
From the second equation, we can express $Q_{f}^{'}$ in terms of $Q_{f}$ :
$Q_{f}^{'} = \frac{3}{2} Q_{f}$
Substituting this into the first equation:
$Q_{f} + \frac{3}{2} Q_{f} = 9$
$\frac{5}{2} Q_{f} = 9$
$Q_{f} = \frac{9 \times 2}{5} = \frac{18}{5} μ C = 3.6 μ C$
Now substituting back to find $Q_{f}^{'}$ :
$Q_{f}^{'} = 9 - Q_{f} = 9 - 3.6 = 5.4 μ C$
Final Charges
Thus, the final charges on the spheres are:
- Charge on $S_{1}$ ( $Q_{f}$ ) = $3.6 μ C$
- Charge on $S_{2}$ ( $Q_{f}^{'}$ ) = $5.4 μ C$

Updated on:7/8/2024

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two metal spheres A and B of radii a & b (a $<$ b) respectively are at a large distance apart. Each sphere carries a charge of 100 $μ_{C}$ the sphere are connected by a conducting wire, then
ACharge will flow from A to B
BCharge will flow from B to A
CNO charge flows in the wire
DAll charges will reside on the connecting wire
Two small conducting spheres of equal radius have charges $+ 10 μ C$ and $- 20 μ C$ respectively and placed at a distance R from each other. They experience force $F_{1}$ . If they are brought in contact and separated to the same distance, they experience force $F_{2}$ . The ratio of $F_{1}$ to $F_{2}$ is
A $1 : 8$
B $- 8 : 1$
C $1 : 2$
D $- 2 : 1$
Paragraph for Questions 53 and 54: An isolated system consists of two conducting spheres A and B. Sphere A has five times the radius of sphere B. Initially, the spheres are given equal amounts of positive charge and are isolated from each other. The two spheres are then connected by a conducting wire.
Note: The potential of a sphere of radius R that carries a charge $Q$ is $V = k Q / R$ , if the potential at infinity is zero.
Determine the ratio of the charge on sphere A to that on sphere $B, q_{A} / q_{B}$ , after the spheres are connected by the wire.
A1
B $1 / 5$
C $5$
D $25$

JEE MAINS PREVIOUS YEAR-JEE MAINS 2020-PHYSICS

Home
Ask Doubt
Profile