Two metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
q1/q2=R21/R22
q1/q2=R1/R2
q1/q2=R31/R32
q1/q2=(R21−R22)/(R21+R22)
The correct Answer is:2
To solve the problem, we need to analyze the situation of two metallic spheres connected by a thin wire. When two conductors are connected by a wire, they will have the same electric potential.
1. Understanding the System:
We have two metallic spheres with radii R1 and R2, and they carry charges +q1 and +q2 respectively. Since they are connected by a wire, they must be at the same electric potential.
2. Electric Potential of a Sphere:
The electric potential V of a charged metallic sphere is given by the formula:
V=Q4πϵ0R
where Q is the charge on the sphere, R is the radius of the sphere, and ϵ0 is the permittivity of free space.
3. Setting Up the Equations:
For sphere 1 (radius R1 and charge q1):
V1=q14πϵ0R1
For sphere 2 (radius R2 and charge q2):
V2=q24πϵ0R2
4. Equating the Potentials:
Since the spheres are connected by a wire, their potentials are equal:
V1=V2
Substituting the expressions for V1 and V2:
q14πϵ0R1=q24πϵ0R2
5. Simplifying the Equation:
The 4πϵ0 cancels out from both sides:
q1R1=q2R2
6. Finding the Relationship Between Charges:
Rearranging the equation gives us:
q1q2=R1R2
This means that the ratio of the charges on the two spheres is equal to the ratio of their radii.
Final Result:
q1q2=R1R2
We have two metallic spheres with radii R1 and R2, and they carry charges +q1 and +q2 respectively. Since they are connected by a wire, they must be at the same electric potential.
The electric potential V of a charged metallic sphere is given by the formula:
V=Q4πϵ0R
where Q is the charge on the sphere, R is the radius of the sphere, and ϵ0 is the permittivity of free space.
For sphere 1 (radius R1 and charge q1):
V1=q14πϵ0R1
For sphere 2 (radius R2 and charge q2):
V2=q24πϵ0R2
Since the spheres are connected by a wire, their potentials are equal:
V1=V2
Substituting the expressions for V1 and V2:
q14πϵ0R1=q24πϵ0R2
The 4πϵ0 cancels out from both sides:
q1R1=q2R2
Rearranging the equation gives us:
q1q2=R1R2
This means that the ratio of the charges on the two spheres is equal to the ratio of their radii.
q1q2=R1R2
Topper's Solved these Questions
Similar Questions
(a) Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d.
(b) Two charged spherical conductors of radii R1 and R2 when connected by a conducting wire acquire charges q1andq2 respectively. Find the ratio of their surface charge densities in terms of their radii.
View SolutionTwo chareged sperical conductors of radill R1andR2 when connected by a connecting wire acquire charges q1andq2 respectively. Find the ratio of their charge densities in terms of their radil ?
View Solution
Knowledge Check
The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
ANo change in the electrical energy of the systemBAn increase in the electrical energy of the systemCAlways a decrease in the electrical energy of the systemDA decrease in electrical energy of the system until Q1R2=Q2R3Consider a system composed of two metallic spheres of radii r1andr2 conneced by a thin wire and switch S as shown in the figure. Initially S is in open position. And the spheres carry charges q1andq2 respectively. If the switch is closed, the potential of the system is
 A14πε0q1q2r1r2B14πε0(q1+q2r1+r2)C14πε0(q1r1+q2r2)D14πε0(q1+q2√r1r2)
A14πε0q1q2r1r2B14πε0(q1+q2r1+r2)C14πε0(q1r1+q2r2)D14πε0(q1+q2√r1r2)Passage III
Two small metallic spheres of radii r1andr2 carry charges q1andq2, respectively such that they have the same polarity. Both the spheres are widely separated from each other and then the two are connected by a metallic wire.
Answer the following questions:
If σ1andσ2 are the corresponding surface charge desities of both the spheres then σ1/σ2 isAr1/r2Br2/r1C2DNone of these
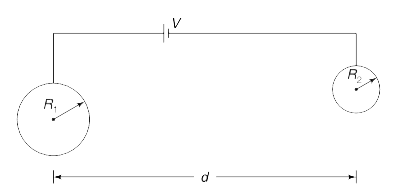
Two solid conducting spheres of radii R1 and R2 are kept at a distance d(>>R1andR2) apart. The two spheres are connected by thin conducting wires to the positive and negative terminals of a battery of emf V. Find the electrostatic force between the two spheres
View SolutionTwo concentric, thin metallic spheres of radii R1 and R2 (R1>R2) bear charges Q1 and Q2 respectively. Then the potential at distance r between R1 and R_(2) will be
View SolutionPassage III
Two small metallic spheres of radii r1andr2 carry charges q1andq2, respectively such that they have the same polarity. Both the spheres are widely separated from each other and then the two are connected by a metallic wire.
Answer the following questions:
If V1andV2 are the corresponding electric potentials of both the spheres then V1/V2 is
View SolutionPassage III
Two small metallic spheres of radii r1andr2 carry charges q1andq2, respectively such that they have the same polarity. Both the spheres are widely separated from each other and then the two are connected by a metallic wire.
Answer the following questions:
If E1andE2 are the corresponding electric fields on surface of both the spheres then E1/E2 is
View SolutionTwo metal spheres of radii R1 and R2 are charged to the same potential. The ratio of charges on the spheres is
View Solution
