If pandq are chosen randomly from the set {1,2,3,4,5,6,7,8,9,10} with replacement, determine the probability that the roots of the equation x2+px+q=0 are real.
Video Solution
Text Solution
The roots of x2+px+q=0 will be real if p2−4q≥0 or p2≥4q.
The possible values of p and q are given in the following table:
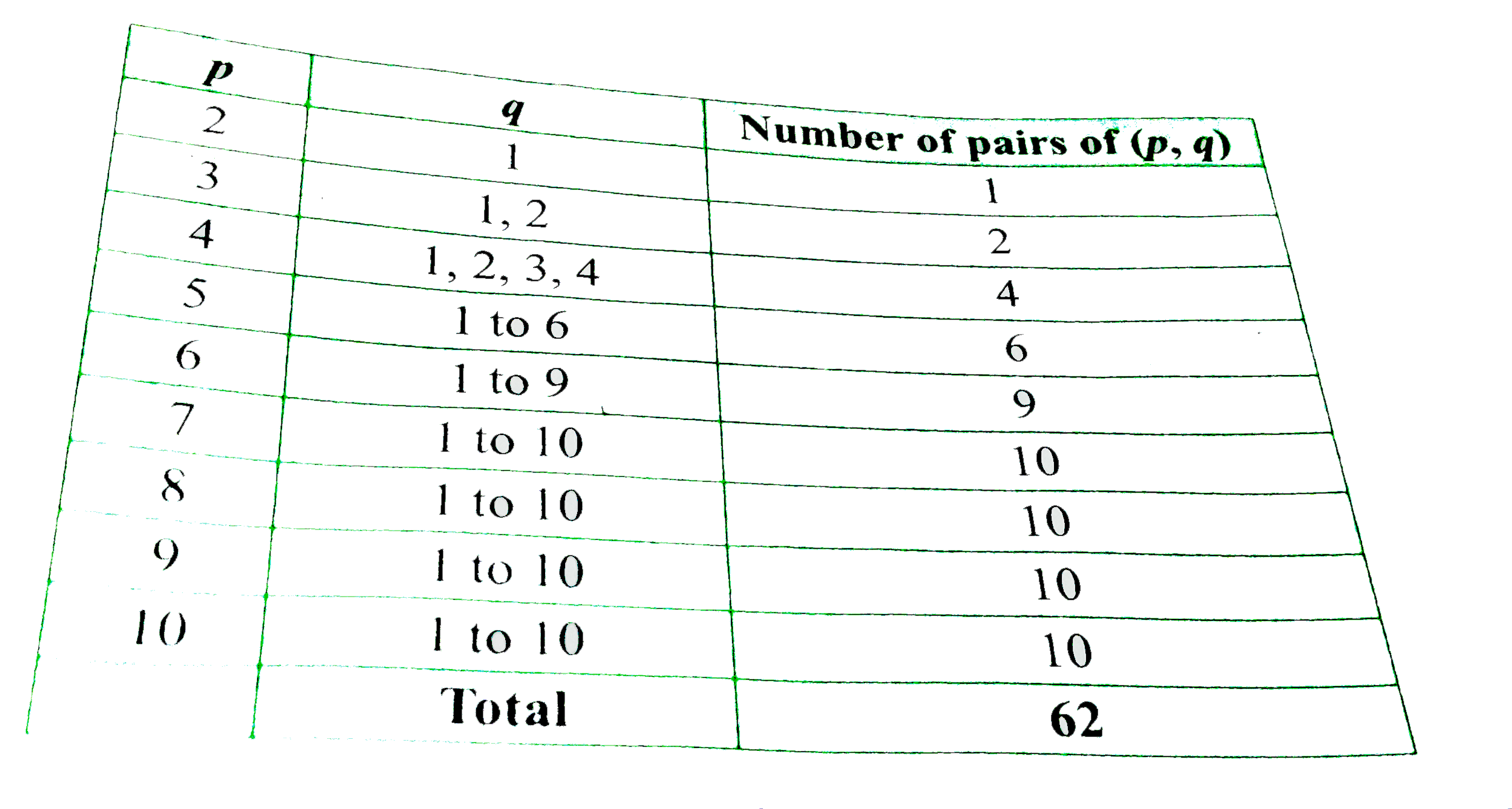
Also, the total number of possible pairs (p,q) = 10 × 10 = 100
∴ Required probability = 62100=0.62
|
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
Similar Questions
Knowledge Check
If p and q are chosen randomly from the set {1, 2, 3, ………, 10} with replacement, then the probability that the roots of the equation x2+px+q=0 are real is
A0.62B0.32C0.44D0.55If p and q are chosen from the set (1, 2, 3, 4, 5, 6, 7, 8, 9, 10), with replacement, the probability that the roots of the equation x2+2px+q=0 are real is
A0.84B0.16C0.62D0.38If two numbers p and q are choosen randomly from the set {1, 2, 3, 4} with replacement, then the probability that p2≥4q is equal to
A14B316C12D716
What is the probability that the roots of the equation x2+x+n=0 are real, where n∈Nandπ<4 ?
View SolutionThe number a, b are chosen from the set(1,2,3,4,5,6,7,8,9,10) with replacement. Probability that a devides b is λ, then 4000λ27is:
View SolutionIf two numbers p and q are choosen randomly from the set {1, 2, 3, 4} with replacement, then the probability that p2≥4q is equal to
View SolutionIf two numbers p and q are choosen randomly from the set {1, 2, 3, 4} with replacement, then the probability that p2≥4q is equal to
View SolutionTwo numbers are chosen from {1, 2, 3, 4, 5, 6, 7, 8} one after another without replacement. Then the probability that
View Solution
