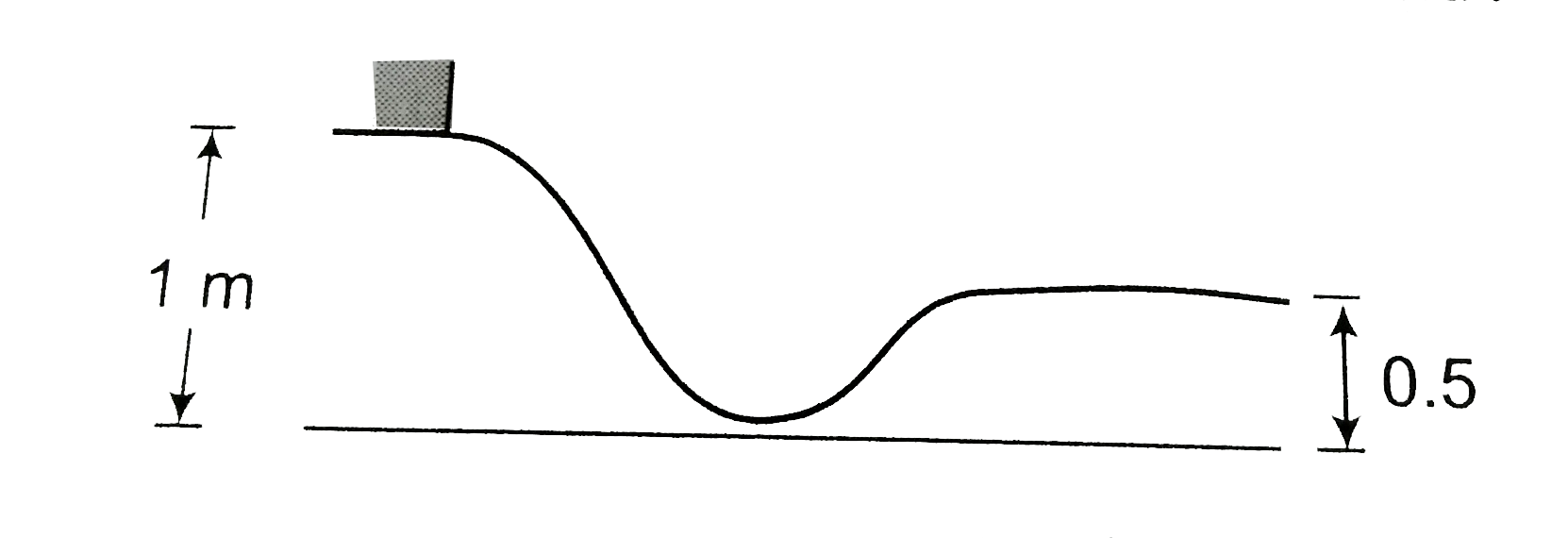
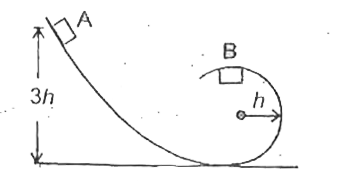
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
Applying the law of conservation of mechanical energy for the points A and B,
mgH=12mv2+mgh
g−v22=g2
orv2=g⇒v=√g=3.1ms−1
After point B the particle exhibits projectile motion with θ=0∘ and y=−0.5m
Horizontal distance travelled by the body
R=u√2hg=3.1×√2×0.59.8=1m
Topper's Solved these Questions
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EVALUATE YOURSELF-1
8 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - Evaluate Yourself - 2
8 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Integer)
12 Videos
Similar Questions
Figure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?
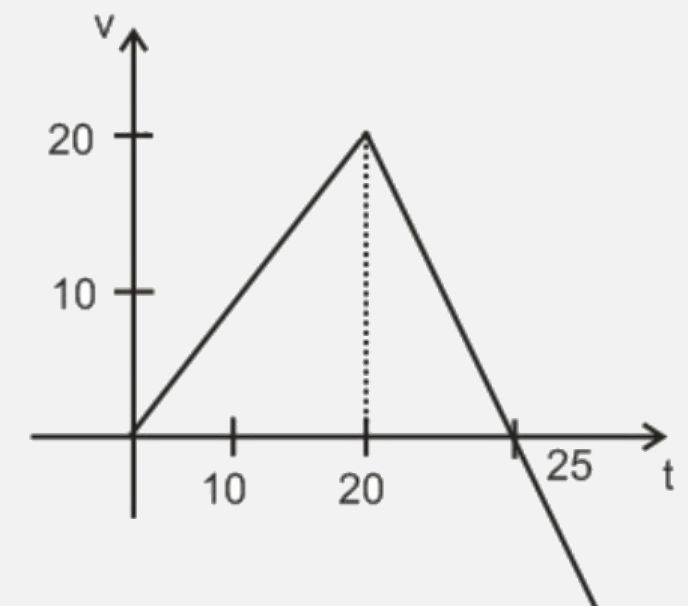
View SolutionThe figure shows the v−t graph of a particle moving in a straight line. Starting from rest, the time after which the particle returns to its starting position is
View Solution
Knowledge Check
The velocity-time graph of a particle in straight line motion is veloity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
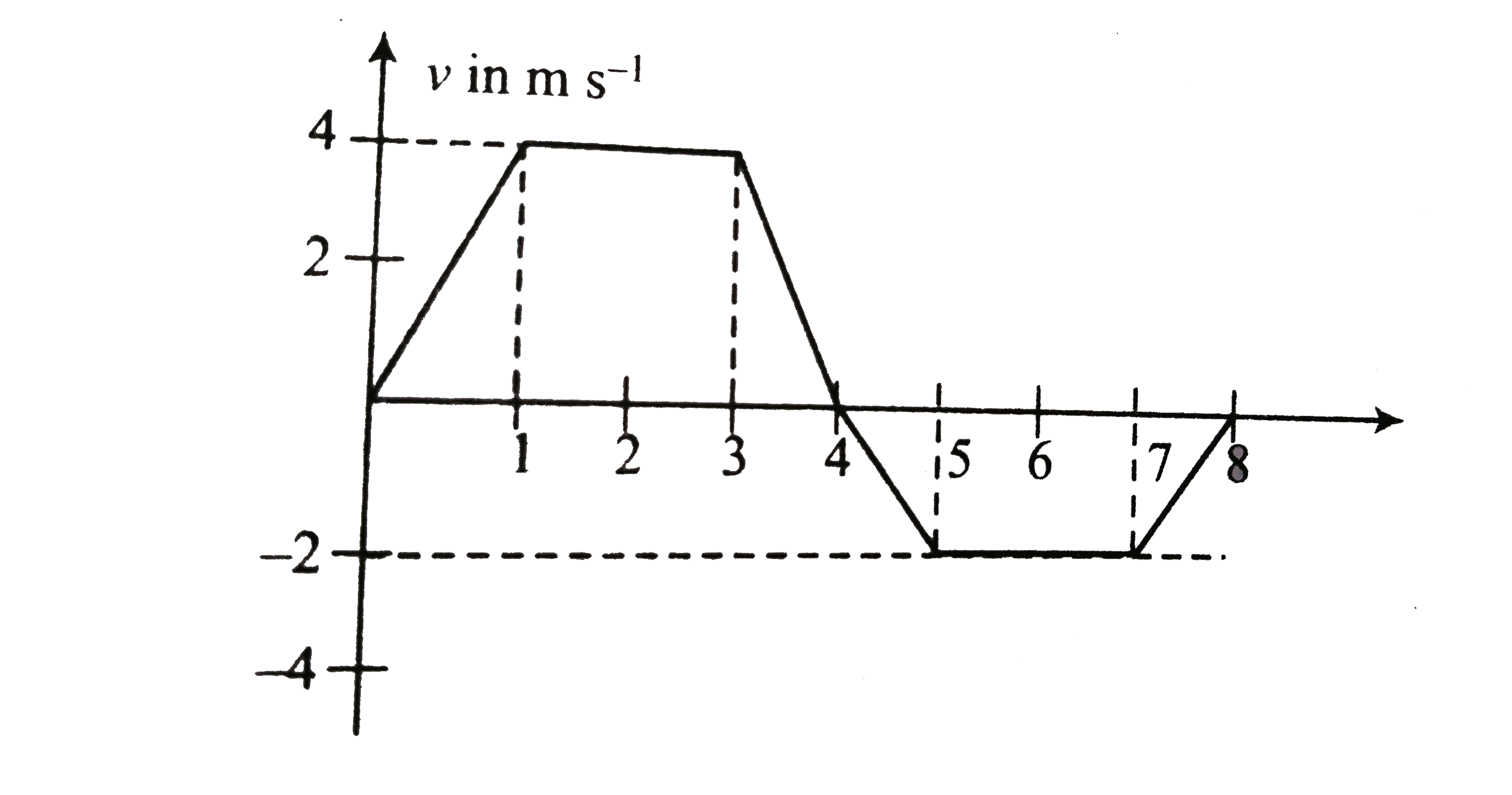 .
.
The distance of the particle from the origin after 8s is .A18mB16mC8mD6mA stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground in
AStraight line pathBCircular pathCParabolic pathDHyperbolic pathA particle travels from A to B path shown in figure, then the displacement of particle is :
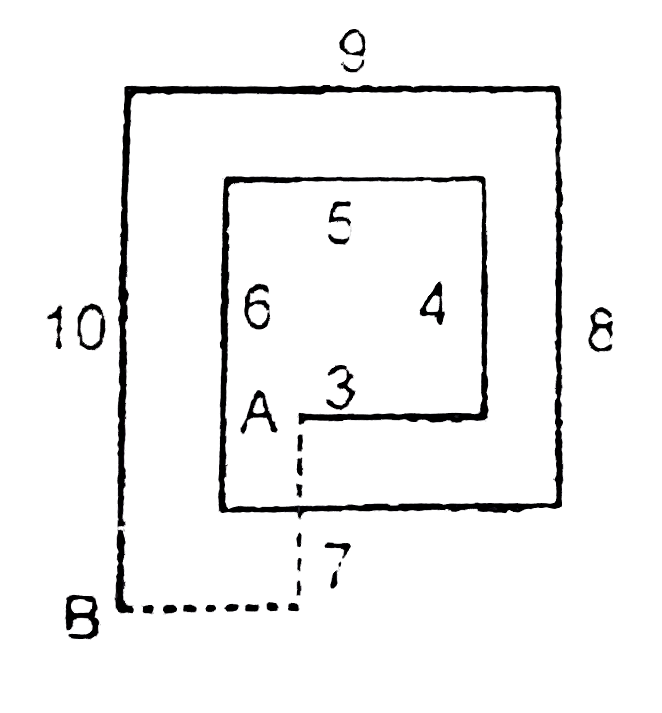 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of these
A particle is projected from point O on level ground towards a smooth vertical wall 50m from O and hits the wall. The initial velocity of the particle is 30m/s at 45° to the horizontal and the coefficient of restitution between the particle and the wall is e. Find the distance from O of the point at which the particle hits the ground again if
e = 0
View SolutionA particle is projected from point O on level ground towards a smooth vertical wall 50m from O and hits the wall. The initial velocity of the particle is 30m/s at 45° to the horizontal and the coefficient of restitution between the particle and the wall is e. Find the distance from O of the point at which the particle hits the ground again if
e = 1
View SolutionA particle is projected from point O on level ground towards a smooth vertical wall 50m from O and hits the wall. The initial velocity of the particle is 30m/s at 45° to the horizontal and the coefficient of restitution between the particle and the wall is e. Find the distance from O of the point at which the particle hits the ground again if
e=1/2
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
View Solution
