Calculate electric flux linked with a sphere of radius 1 m and charge of 1C at its centre.
To calculate the electric flux linked with a sphere of radius 1 m and a charge of 1 C at its center, we can use Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's Law states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed by that surface. Mathematically, it is expressed as:
Φ=Qε0
where:
- Φ is the electric flux,
- Q is the total charge enclosed,
- ε0 is the permittivity of free space, approximately equal to 8.85×10−12C2/N m2.
Step 2: Identify the Charge Enclosed
In this case, the charge enclosed by the Gaussian surface (the sphere) is given as:
Q=1C
Step 3: Substitute the Values into Gauss's Law
Now, we can substitute the values into the equation for electric flux:
Φ=1Cε0
Step 4: Calculate the Electric Flux
Substituting the value of ε0:
Φ=18.85×10−12≈1.13×1011N m2/C
Final Answer
The electric flux linked with the sphere is approximately:
Φ≈1.13×1011N m2/C
---
Gauss's Law states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed by that surface. Mathematically, it is expressed as:
Φ=Qε0
where:
- Φ is the electric flux,
- Q is the total charge enclosed,
- ε0 is the permittivity of free space, approximately equal to 8.85×10−12C2/N m2.
In this case, the charge enclosed by the Gaussian surface (the sphere) is given as:
Q=1C
Now, we can substitute the values into the equation for electric flux:
Φ=1Cε0
Substituting the value of ε0:
Φ=18.85×10−12≈1.13×1011N m2/C
The electric flux linked with the sphere is approximately:
Φ≈1.13×1011N m2/C
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)
59 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
A point charge +Q is placed at a point. Calculate the electric flux associated with one sphere of radius r , which the given point charge at its centre.
View SolutionThere is one hollow sphere of radius 1 m and it contains a charge of 8.85 μC at its centre . Calculate the electric flux linked with the sphere per unit area . Electric flux per unit area is defined as flux density .
View Solution
Knowledge Check
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A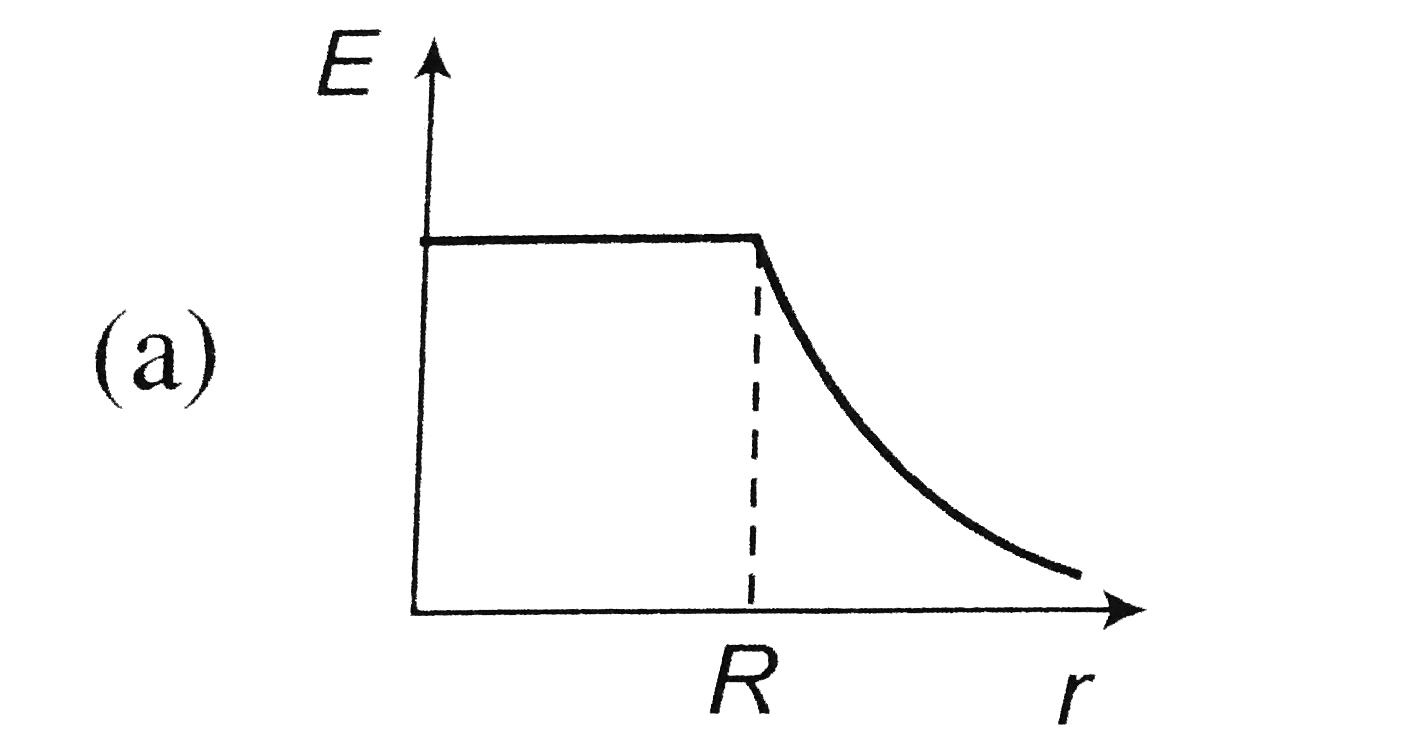 B
B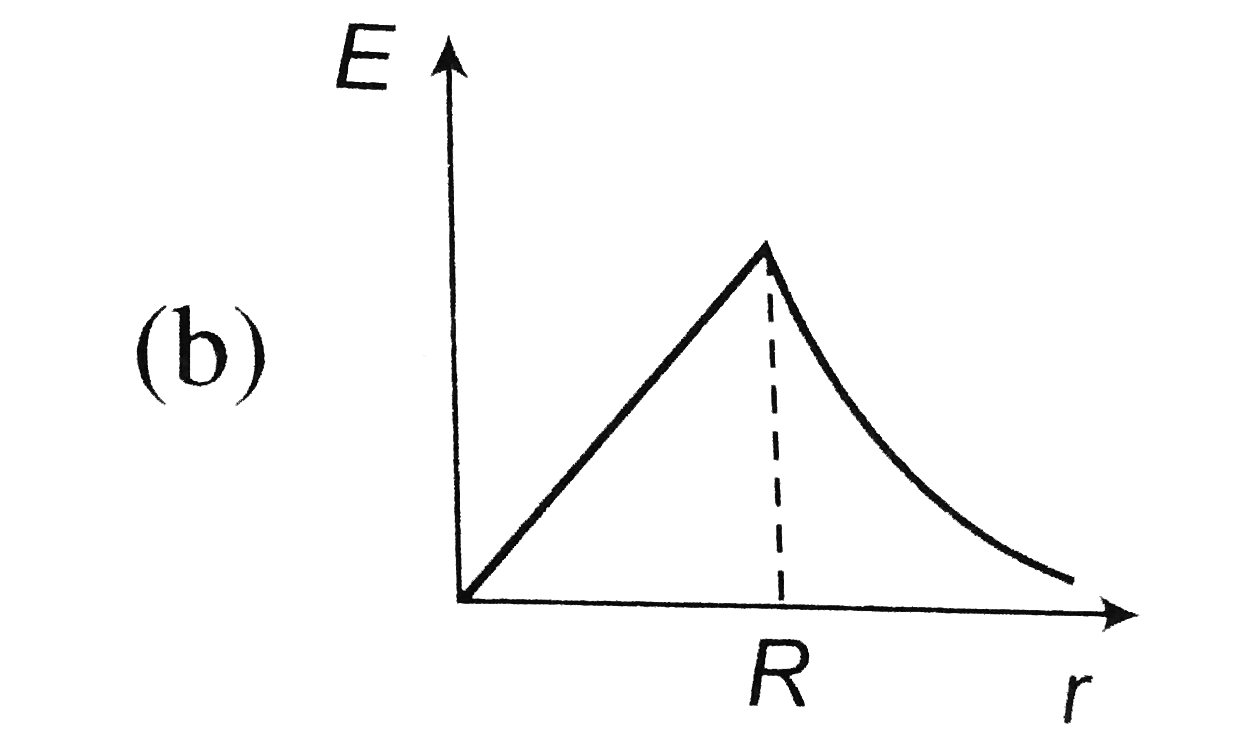 C
C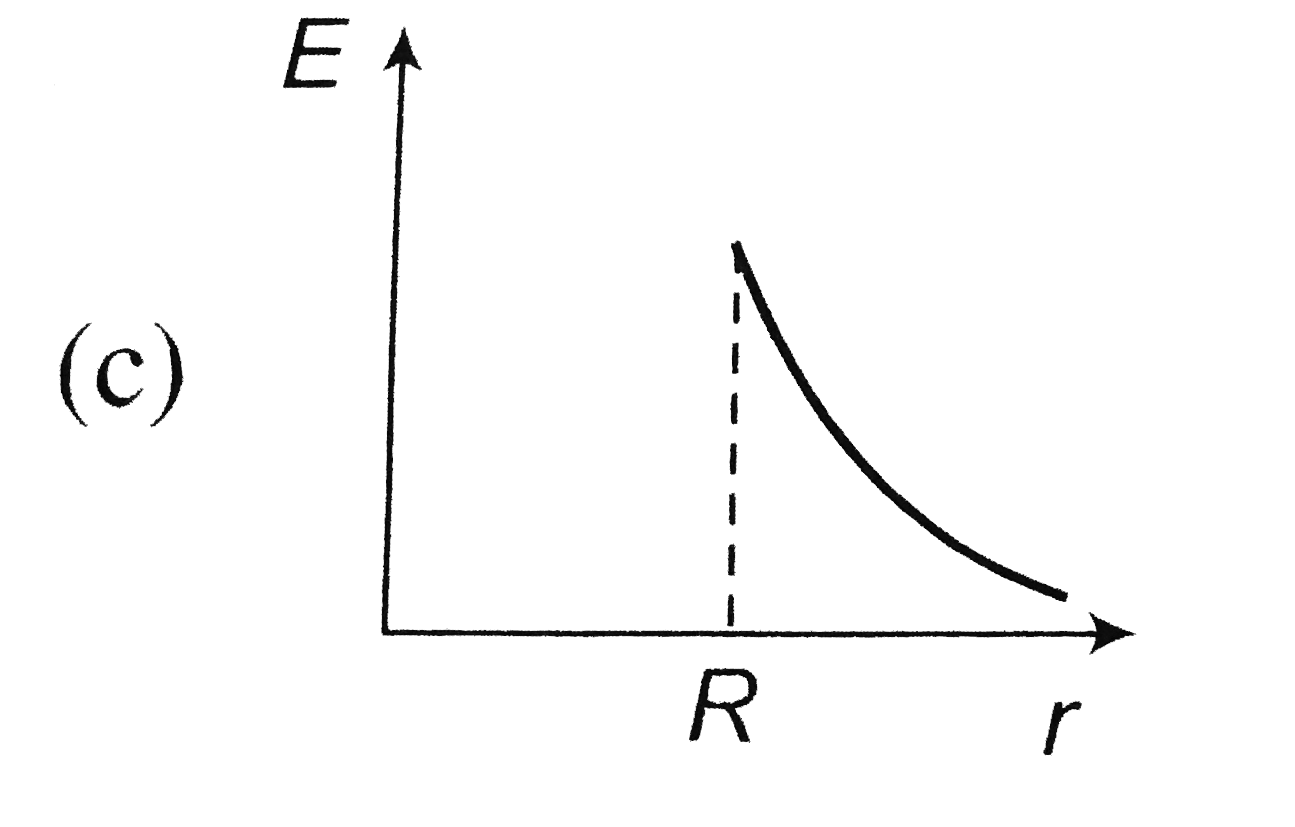 D
D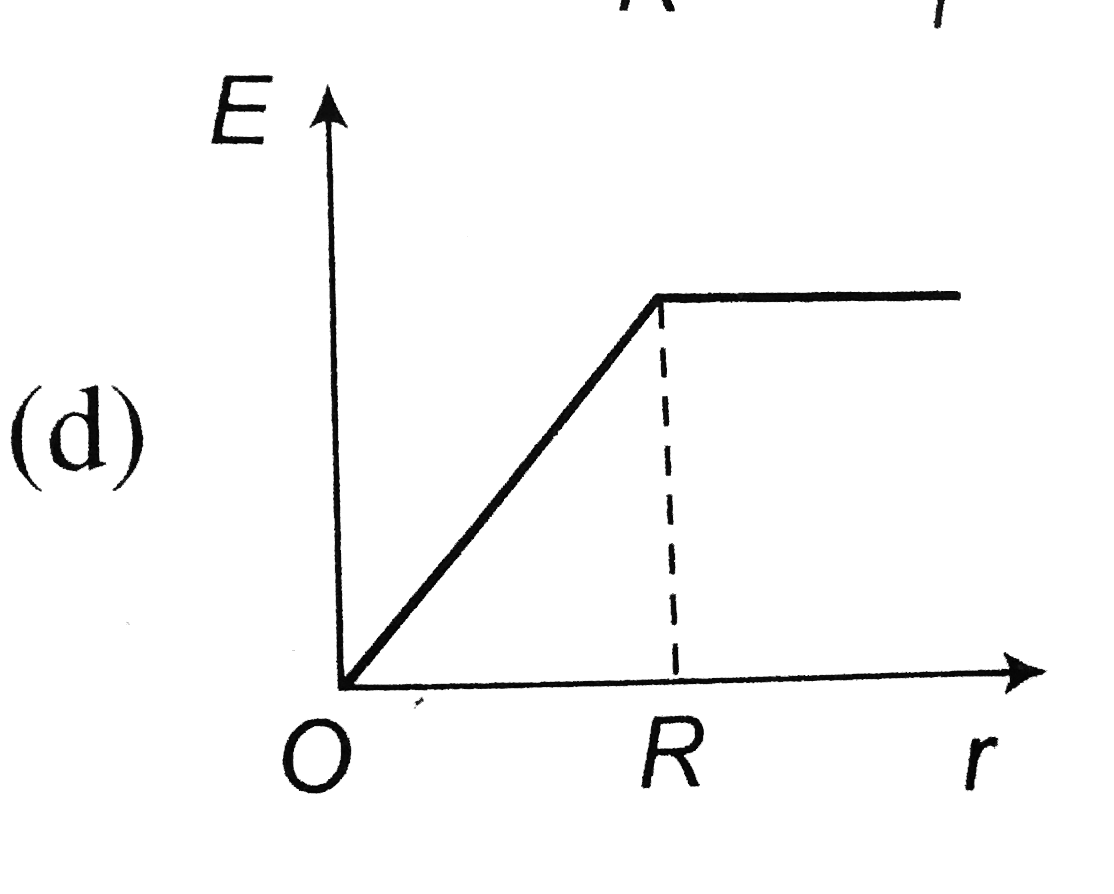
The electric charges are distributed in a small volume. The flux of the electric field through a spherica surface of radius 10 cm surrounding the total charge is 20V−m. The flux over a concentric sphere of radius 20 cm will be
A20 VmB10 VmC40 VmD5 VmGraphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
A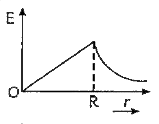 B
B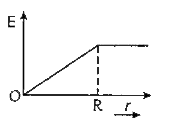 C
C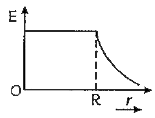 D
D
Net electric flux through a sphere of radius 1 m placed in a uniform electric field as shown in the figure is → E = 103 N/C
View SolutionTwo charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
View SolutionTwo charges of magnitude −2Qand+Q are located at points (a,0) and (4a, 0) respectively ,What is the electric flux due to these charges through a sphere of radius 3a with its centre at the origin?
View SolutionElectric charges are distributed in a small volume.The flux of the electric field through a spherical surface of radius 1m surrounding the total charge is 100V−m.The flux over the concentric sphere of radius 2m will be:
View SolutionThe electric flux emerging out from 1 C charge is
View Solution
