Question

दो घर्षणरहित आनत पथ , जिनमे से एक ही ढाल अधिक है और दूसरे की ढाल कम है , बिंदु पर मिलते है। बिंदु A पर मिलते है। बिंदु A पर मिलते है । बिंदु से प्रत्येक पथ पर एक - एक पत्थर को विरामावस्था से नीचे सरकाया जाता है ( चित्र ) । क्या ये पत्थर को विरामावस्था से नीचे सरकाया जाता है (चित्र) । क्या ये पत्थर एक ही समय पर नीचे पहुँचेगे ? क्या वे वहाँ एक ही चाल से पहुँचेगे ? व्याख्या कीजिये। यदि ${\theta }_1={30}^{\circ },{\theta }_2={60}^{\circ }$ और $h=10m$ दिया है तो दोनों पत्थरो की चाल एवं उनके द्वारा नीचे पहुँचने में लिए गए समय क्या है ?

Explanation

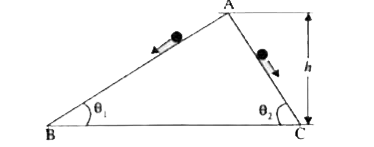
चित्र में OA तथा OB दो चिकने आनत तल है जो क्षैतिज से `theta_(1)`तथा`theta_(2)` कोण बनाते है | दोनों समतलो की ऊँचाई समान है। इस कारण से दोनों पत्थर नीचे समान चाल से पहुँचेगे।

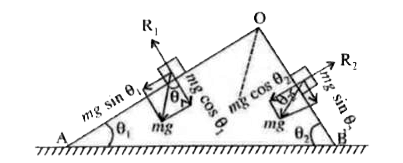
` :. " " P.E = K.E `
` mgh = 1/2 mv_(1)^(2) =1/2 mv_(2)^(2)`
या `v_(1) = v_(2)`
यदि पत्थर (1) व (2) में उत्पन्न त्वरण क्रमशः `a_(1)` तथा `a_(2)` है तब
` a_(1) = g sin theta_(1)` तथा `a_(2) = g sin theta_(2)`
` :' " " theta_(2) gt theta_(1)`
गति के प्रथम समीकरण से
`v = u + at = 0 +at`
या ` t = v/a `
या ` t prop 1/a ` और `a_(2) gt a_(1)`
` :. " " t_(2) lt t_(1)`
अर्थात पहले पत्थर की अपेक्षा दूसरा पत्थर कम समय लेगा और तलहटी पर पहले पहुंचेगा अर्थात झुकाव वाले पत्थर पहले तलहटी पर पहुँचेगा।
दिया गया है - ` h = 10 m ` तब
वेग `v = sqrt(2gh ) = sqrt(2 xx 9.8 xx10)`
` = 14 m/s `
` theta_(1) = 30^(@)` के लिए समय
` v = u + at ` से ,
`v = g sin theta_(1). t_(1)`
`rArr " " t_(1) = v/(g sin theta_(1)) = 14/(9.8 xx1/2)`
` = 14/(4.9) = 2.8 ` सेकंड
या `t_(2) = v/(g sin theta_(2)) = 14/(9.8 xx sin 60^(@))`
`t_(2) = 1.73 ` सेकंड |