A circular loop of rope of length L rotates with uniform angular velocity ω about an axis through its centre on a horizontal smooth platform. Velocity of pulse (with resppect to rope ) produce due to slight radiul displacement is given by

ωL
ωL2π
ωLπ
ωL4π2
The correct Answer is:B
Step by step video, text & image solution for A circular loop of rope of length L rotates with uniform angular velocity omega about an axis through its centre on a horizontal smooth platform. Velocity of pulse (with resppect to rope ) produce due to slight radiul displacement is given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART II
19 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART III
15 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART II
7 Videos
- WAVE OPTICSBOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod.
View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.
View Solution
Knowledge Check
A heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchangedA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ωA cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
AparabolaBellipticalCcircularDspherical
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionThe body is rotating with uniform angular velocity (ω ) having rotational kinetic energy ( E) . Its angular momentum (L ) is :
View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity ωrad s−1 as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is

View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
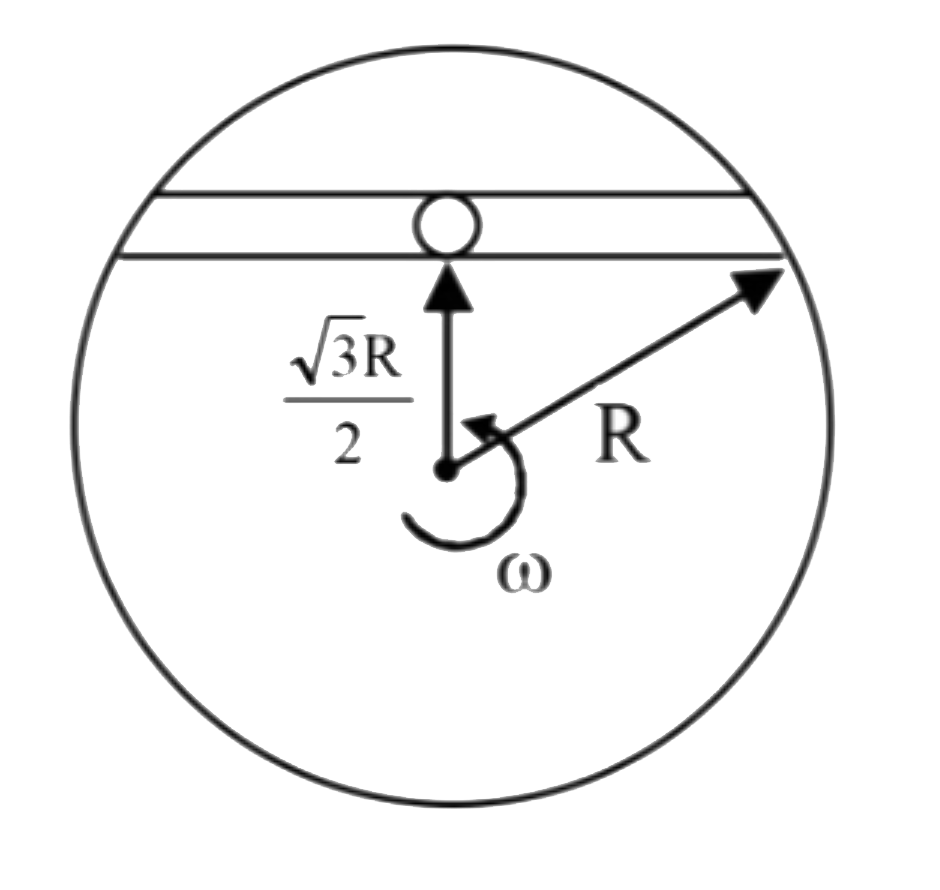
View SolutionA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
View Solution
