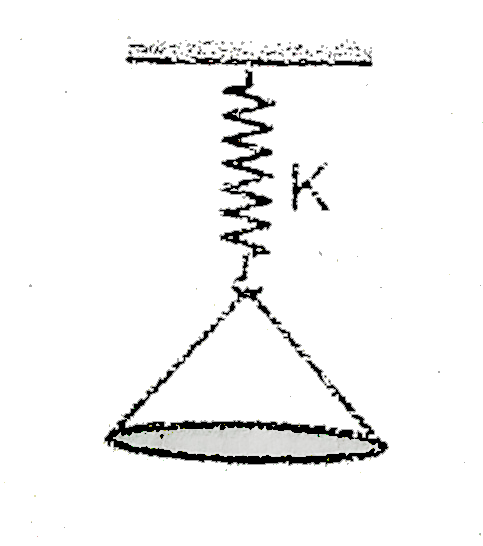
A block of mass m is suspended from the ceiling of a stationary standig elevator through a spring of spring constant k. Suddenly, the cable breaks and the elevator starts falling freely. Show that the bklock now executes a simple harmonic motion of amplitude $m \frac{g}{k}$ in the elevator

Video Solution

Text Solution

Verified by Experts

When the elevator is stationary, the spring is stretched to support the block. If the extension is $x$ , the tension is $k x$ which should balance the weight of the block.

Thus, $x = m g / k$ . As the cable breaks, the elevatore starts falling with accelertion $' g'$ . We shall work in the frame of reference of the elevator. Then we have to use pseudo force $m g$ upward on the blod This force will balance the weight. Thus, the block is subjected to a net force $k x$ by the spring when it is at a distance $x$ from the position of unstretched spring. Hence, its motion inthe elevatore simple harmonic with its mean position corresponding to the unstretched spring. initially, the spring is stretched by $x = m g / k$ , where the velocity of the block (with respect to the elevator) is zero. Thus the amplitude of the resulting simple harmonic motion is $m g / k$ .

Updated on:21/07/2023

A solid ball of mass $m$ is made to fail from a height $H$ on a pan suspended through a spring of spring constant $K$ as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is

A $\frac{m g}{K}$
B $\frac{m g}{k} {(1 + \frac{2 H K}{m g})}^{1 / 2}$
C $\frac{m g}{K} + {(\frac{2 H K}{m g})}^{1 / 2}$
D $\frac{m g}{K} [1 + {(1 + \frac{2 H K}{m g})}^{1 / 2}]$
A weight is suspended from the ceiling of a lift by a spring balance. When the lift is stationary the spring balance reads W . If the lift suddenly falls freely under gravity, the reading on the spring balance will be
A $W$
B $2 W$
C $W / 2$
D $0$
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

A $\frac{m g}{k}$
B $\frac{m g}{k} \sqrt{1 + \frac{2 h k}{m g}}$
C $\frac{m g}{k} + \frac{m g}{k} \sqrt{\frac{1 + 2 h k}{m g}}$
DNone of these