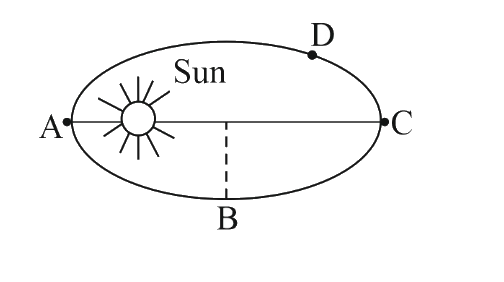
Accoding to kelper's law if a planet revolves around the sun, its trajectory is elliptical with sun sweeps equal areas is equal interyals of time. Given the ratio f magnetitude of maximum velocity (u) to minimum velocity (v) of planet as 3 and shortance distance between plonet and sun is $\frac{a}{2}$ .
If velocity at the end of axis of the elliptical orbit is v. then magnetiduce of u, v,v are in

A

A.P

B

H.P

C

G.P

D

none of these

Text Solution

Verified by Experts

The correct Answer is:C

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Accoding to kelper's law if a planet revolves around the sun, its trajectory is elliptical with sun sweeps equal areas is equal interyals of time. Given the ratio f magnetitude of maximum velocity (u) to minimum velocity (v) of planet as 3 and shortance distance between plonet and sun is $\frac{a}{2}$ .
Elccentricity of elliptical orbit is
A $\frac{2}{3}$
B $\frac{2}{4}$
C $\frac{2}{1}$
D $\frac{1}{\sqrt{2}}$
Question 2 - Select One
Accoding to kelper's law if a planet revolves around the sun, its trajectory is elliptical with sun sweeps equal areas is equal interyals of time. Given the ratio f magnetitude of maximum velocity (u) to minimum velocity (v) of planet as 3 and shortance distance between plonet and sun is $\frac{a}{2}$ .
Time taken by planet two revolves once is $\frac{k a}{u}$ then k is
A $π$
B $2 \sqrt{3} π$
C $\frac{\sqrt{3}}{2} π$
Dnone of these
Question 3 - Select One
A planet is revolving around the sun as shown in elliptical path. The correct option is

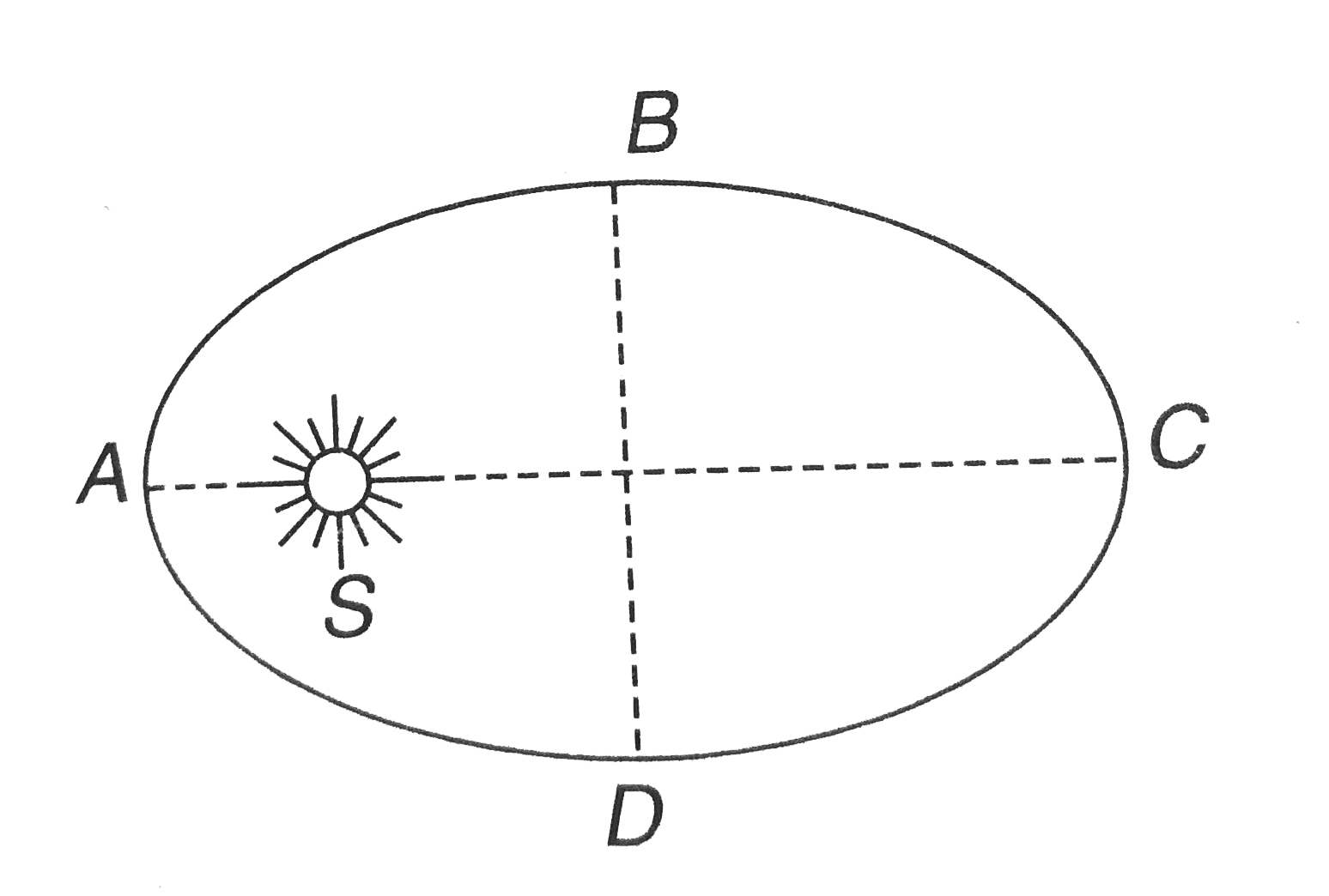AThe time taken in travelling DAB is less than that for BCD
BThe time taken in travelling DAB is greater than that for BCD
CThe time taken in travelling CDA is less than that for ABC
DThe time taken in travelling CDA is greater than that for ABC

FIITJEE-ELLIPSE-COMPREHENSIONS II

Home
Ask Doubt
Profile