Water flows through a tunnel from the reservior of a dam towards the turbine installed in its power plant . The power plant is situated h metre below the reservoir . If the ratio of the cross sectional areas of the tunnel at the resercoir and power station end is , find the speed of the water entering into the turbine .
To solve the problem of finding the speed of water entering the turbine, we will use the principles of fluid mechanics, specifically the continuity equation and Bernoulli's equation. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a reservoir of water at a height h above the turbine. The cross-sectional areas of the tunnel at the reservoir and at the turbine are given as A1 and A2 respectively. The ratio of these areas is given as η=A1A2.
Step 2: Apply the Continuity Equation
The continuity equation states that the mass flow rate must remain constant. Therefore, we can write:
A1V1=A2V2
From this, we can express V1 in terms of V2:
V1=A2A1V2=V2η
Step 3: Apply Bernoulli's Equation
According to Bernoulli's principle, for points 1 (reservoir) and 2 (turbine):
P1ρg+V212g+z1=P2ρg+V222g+z2
Since both points are at the free surface of the water, P1=P2=Patm and the heights are z1=h and z2=0. Thus, we can simplify the equation:
V212g+h=V222g
Step 4: Substitute V1 into Bernoulli's Equation
Substituting V1=V2η into the Bernoulli equation:
12g(V2η)2+h=V222g
This simplifies to:
V222gη2+h=V222g
Step 5: Rearranging the Equation
Rearranging gives:
h=V222g−V222gη2
Factoring out V222g:
h=V222g(1−1η2)
Step 6: Solve for V22
Now, we can solve for V22:
V22=2gh1−1η2
This can be rewritten as:
V22=2ghη2η2−1
Step 7: Find V2
Taking the square root gives:
V2=√2ghη2η2−1
Final Answer
Thus, the speed of the water entering the turbine is:
V2=√2ghη2η2−1
We have a reservoir of water at a height h above the turbine. The cross-sectional areas of the tunnel at the reservoir and at the turbine are given as A1 and A2 respectively. The ratio of these areas is given as η=A1A2.
The continuity equation states that the mass flow rate must remain constant. Therefore, we can write:
A1V1=A2V2
From this, we can express V1 in terms of V2:
V1=A2A1V2=V2η
According to Bernoulli's principle, for points 1 (reservoir) and 2 (turbine):
P1ρg+V212g+z1=P2ρg+V222g+z2
Since both points are at the free surface of the water, P1=P2=Patm and the heights are z1=h and z2=0. Thus, we can simplify the equation:
V212g+h=V222g
Substituting V1=V2η into the Bernoulli equation:
12g(V2η)2+h=V222g
This simplifies to:
V222gη2+h=V222g
Rearranging gives:
h=V222g−V222gη2
Factoring out V222g:
h=V222g(1−1η2)
Now, we can solve for V22:
V22=2gh1−1η2
This can be rewritten as:
V22=2ghη2η2−1
Taking the square root gives:
V2=√2ghη2η2−1
Thus, the speed of the water entering the turbine is:
V2=√2ghη2η2−1
Topper's Solved these Questions
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (OBJECTIVE ) LEVEL I
Explore 40 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (OBJECTIVE ) ASSERTION REASONING TYPE LEVEL -I
Explore 1 Video
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) TRUE OR FALSE QUESTIONS (LEVEL-I)
Explore 6 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
Similar Questions
Water leaks out from an open tank through a hole of area 2mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis 0.4m2. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.
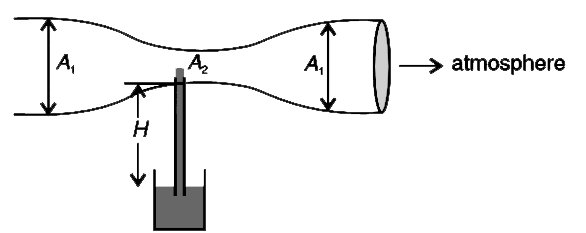
View Solution(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
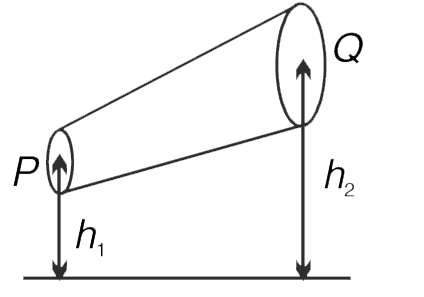
View Solution
Knowledge Check
In hydroelectric power plant, the _____________ energy of the flowing water drives the turbine.
AchemicalBpotentialCkineticDLightThe beaver had made a dam about hundred yards long, and it had formed out of the quickly flowing stream, a wide stretch of water about twelve feet deep. The dam was so firm and broad that it was easy for me to walk along it. After a hundred and fifty yards I came to a 'beaver's castle'- a great heap of logs skilfully fitted together, the lower part covered with earth and plants. The upper logs were put loosely together so that the air could pass through to the interior.
In the late autumn, before land and water are covered with snow and ice, the beaver has to make its dwelling frostproof. It collects young trees and gnaws the stems in a double cone until the tree falls.Then the long stems are gnawed into small sections, the thin twigs bitten off and the logs are dragged to the dwelling. There, the timber is piled on the castle, sometimes to a height of ten or twelve feet. Mud is brought up from the bottom of the lake and packed between the logs with the animal's clever forepaws. The interior is lined with the finest wood shavings. In this tall shelter, the beaver remains high and dry, and protected from frost throughout the winter.
The only access to the dwelling is under the water, and even the forest wolves are not able to pull the firm building apart. The water is the beaver's element. On land it moves slowly and awkwardly. Thus, it is vital for the beaver to have water in which it can swim, and where nature
has not provided this condition for it, it creates it with its dam.
The beaver's activities can change whole landscapes. With this dam, for instance, on which I was standing, beavers had turned a whole wooded alley into a lake, trees that stood there ha been killed by the water and had disappeared. Aquatic game had settled there. Ducks swam past us, and great must have been the number of fish, as swarms of trout had swum past me in the clear stream. Wide stretches of meadow had come into existence on the banks, with flat landing places to which the well-beaten beaver tracks led. Many years of building, gnawing and dragging must have gone into the completion of this immense task, creating a new region for the beaver to live in.
What evidence in the passage suggests that beavers build strong dwellings ?AThe beaver's dwelling is frostproof.BIt takes many years of hard work to build the dwelling.CEven the forest wolves cannot pull the dwelling apart.DThe interior is lined with finest wood shavings.
There are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal
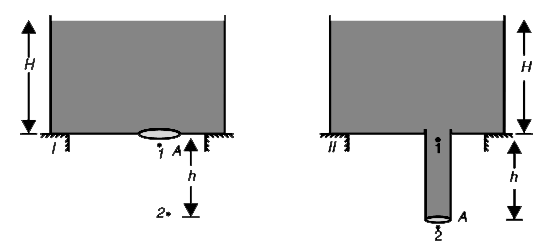
to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe)
(a) Find the speed of flow at point 2 in both figures.
(b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure.
(c) Find the difference in pressure at point 1 in both figures.
View SolutionA pump draws water from a reservoir and sends it through a horizontal pipe with speed v. Find the relation between power of the pump and velocity of liquid.
View SolutionWater from the bottom of a dam of depth h comes out through a narrow pipe and strikes continuousy the tips of the blades of a water turbine. The length of each blade is R. Calculate the most advantaneous speed of rotation of the turbine
[Hint : The most advantageous speed corresponds to the development of maximum power in the turbine]
View SolutionAt a hydroelectric power plant, water is directed at high speed against turbine blades on an axle that turns an electric generatior. For maximum power generation, should the turbine blades be desigened so that the water is brought to a dead stop, or so that the water rebounds?
View Solution(a) Draw the diagram of a device which is used to decrease high S voltage into a AC voltage and state its working principle. Write four sources of energy loss in this device.
(b) A small town with a demand of 1200 kW of electric power at 220 V is situated 20 Km away from an electric plant generating power at 440V. The resistance of the two wire line carrying power is 0.5Ω per km. The town gets the power from the line through a 4000-220 V step-down transformer at s sub-station in the town. Estimate the line power loss in the from of heat.
View SolutionA water heater has a well insulated vertical cylindrical container of radius a in which water is filled to a height h. A resistor made of an allow is used to heat the water in the tank from a temperature θ1 to θ2(>θ1) in a time interval Δt. The resistor wire has cross sectional radius b and its alloy material has resistivity ρ. Calculate the length of the resistor wire. Density and specific heat capacity of water are dands respectively. The power source connected to the resistor has emf ε.
View Solution

