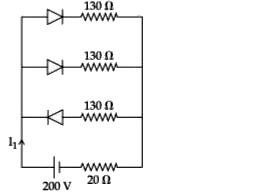
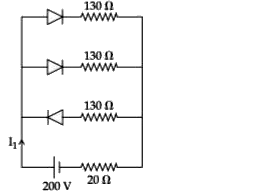
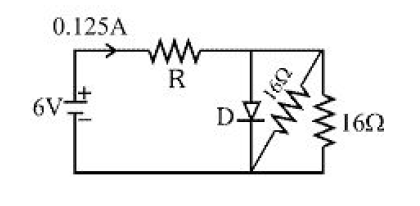
If each diode in figure has a forward has a forward bias resistance of 25 Omega and infinite resistance in reverse bias, what will be the values of the current I1,I2,I3andI4?
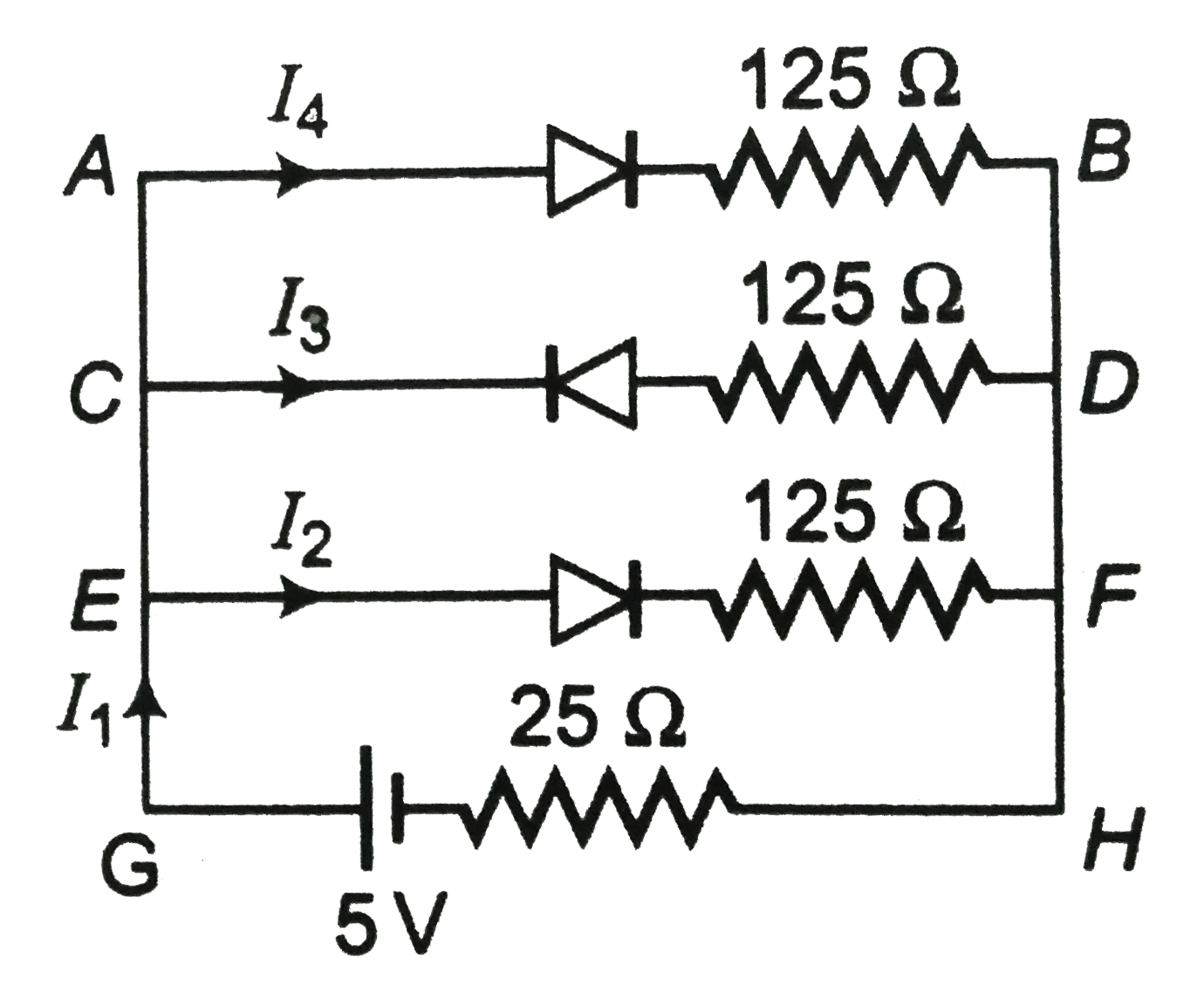
I2=0.40A,I4=0.025A
I2=0.25A,I4=0.20A
I1=0.05A,I3=0.02A
I2=I4=0.025A
The correct Answer is:D
Let R be the effective resistance of the circuit, then
R=(RAB∣∣REF)+25
RAB=125+25=150Ω,REF=125+25=150Ω
∴R=25+1502=100Ω
Since diode in the branch CD is reverse biased, I3=0
Current, I1=5100=0.05A
According to Kirchhoff's current rule,
I1=I2+I3+I4 or I2+I4=I1=0.05A
∵RAB=REF,so,I4=I2
2I4=2I4=0.05,I4=I2=0.052=0.025A
Topper's Solved these Questions
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - NCERT Exemplar
8 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Digital Electronics And Logic Gates
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assertion And Reason
15 Videos
- WAVE OPTICSBOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The resitance of the diode in forward bias condition is 20Ω and infinity in the reverse biased condition. The current in the circuit is
 A0.08AB0.1AC0.04ADzero
A0.08AB0.1AC0.04ADzeroThe circuit shown in the figure contains two diodes each with a forward resistance of 30 Ω and with infinite backward resistance. If the battery is 3 V, the current through the 50 Ω resistance (in ampere) is
 AzeroB0.01C0.02D0.03
AzeroB0.01C0.02D0.03The circuit shown in the figure contains two diodes each with a forward resistance of 30 Ω and with infinite backward resistance. If the battery is 3 V, the current through the 50 Ω resistance (in ampere) is
 AZeroB0.01C0.02D0.03
AZeroB0.01C0.02D0.03
In the given circuit, the diode has a forward resistance of 8 Ω and infinite backward resistance. The value of R is :-
View SolutionAssume that each diode shown has a forward bias resistance of 50Ω and an infinite reverse bias resistance. The current through the resistance 150Ω is
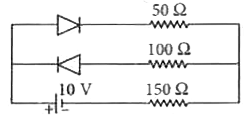
View SolutionA p-n junction offers a high resistance in forward bias and a low resistance is reverse bias.
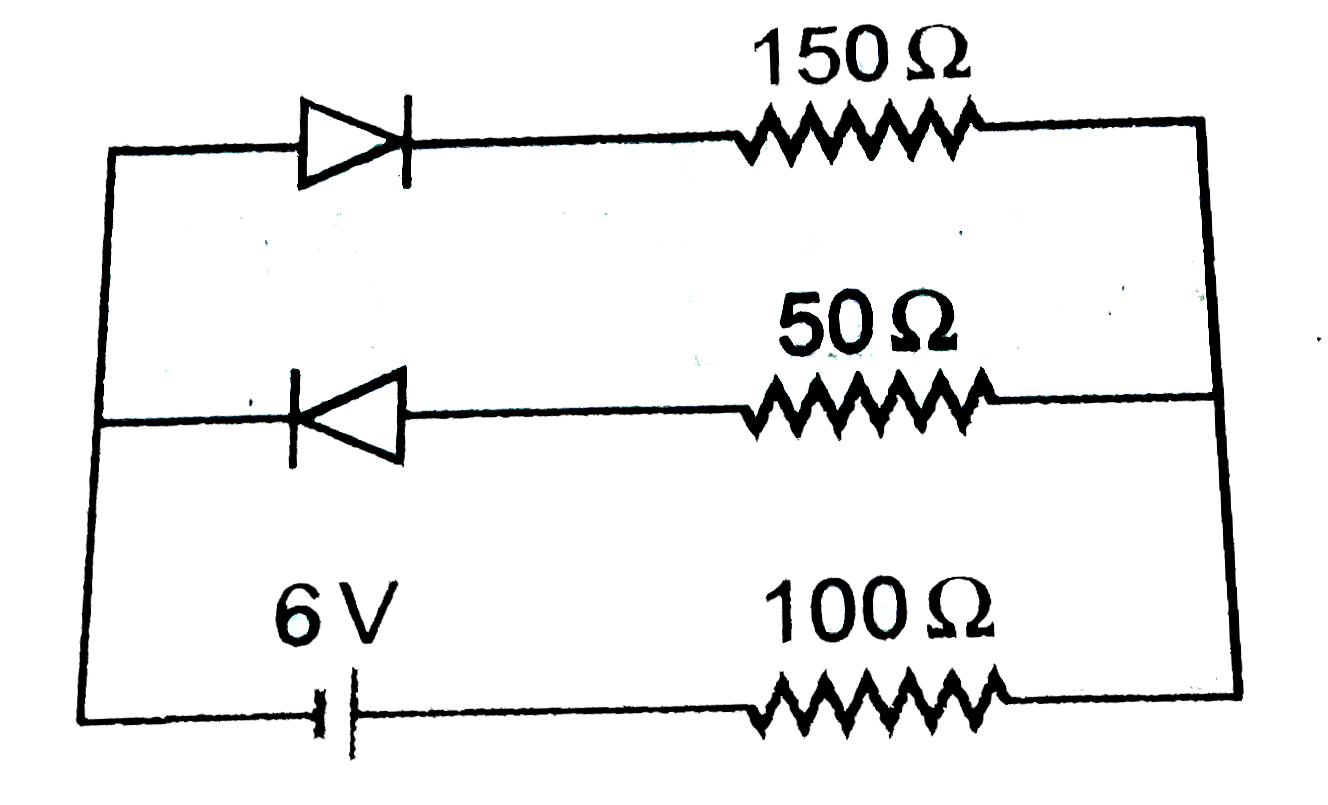
View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50 Ω and with infinite backward resistance. If the battery is 6 V, the current through the 100 Ω resistance (in ampere) is
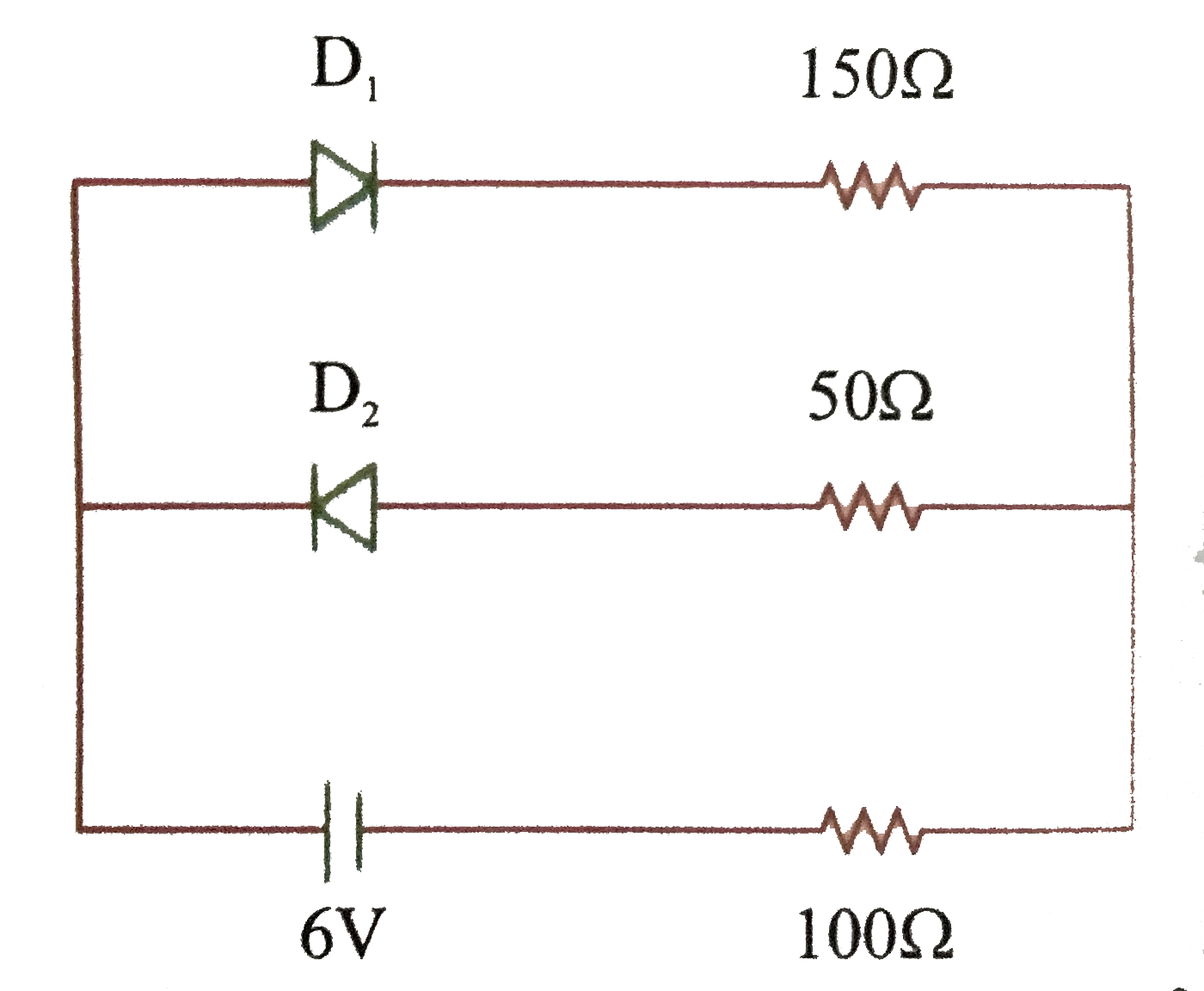
View SolutionThe circuit shown in figure (1) Contains two diodes each with a forward resistance of 50ohm and with infinite reverse resistance. If the battery voltage is 6V, the current through the 100ohm resistance is.
 .
.
View Solution