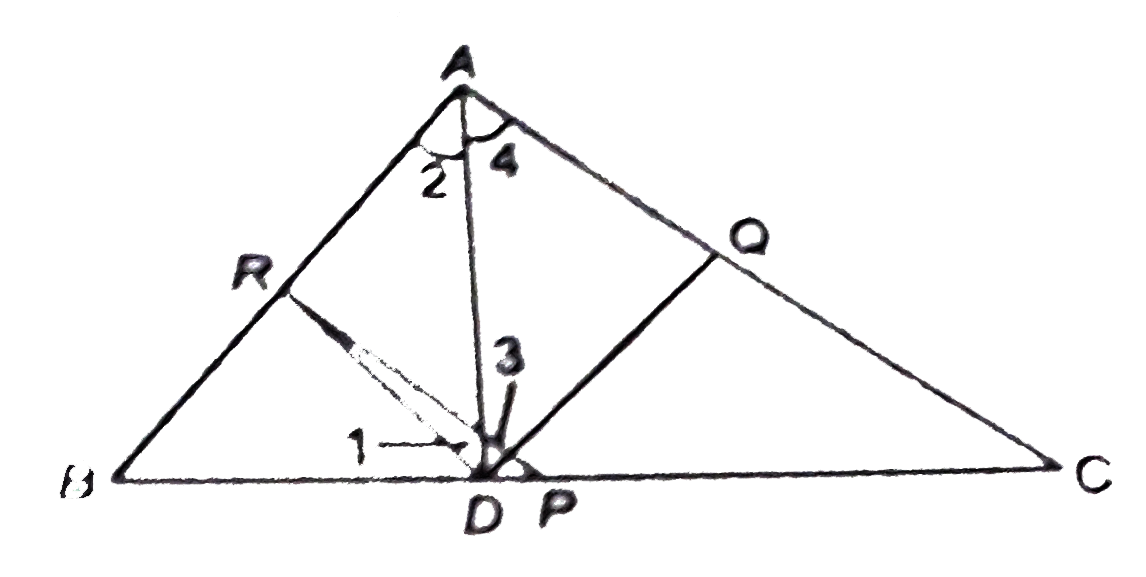
If P, Q and R are the mid-points of the sides, BC, CA and AB of a triangle and AD is the perpendicular from A on BC, then prove that P, Q, R and D are concyclic.
We have to prove that R,D,P and Q are concyclic.
Join RD, QD,PR and PQ.
Since, RP joins R and P, the mid-point of AB and BC.
∴RP| |AC (mid-point theorem)
Similarly, PQ| |AC
Therefore, ARPQ is parallelogram.
So, ∠RAQ=∠RPQ (opposite angles of a parallelogram.....(1)
Since, ABD is a right-angled triangle and DR is a median.
∴RA=DR and ∠1=∠2 ......(2)
Similarly , ∠3=∠4........(3)
Adding eqs. (2) and (3) , we get
∠1+∠3=∠2+∠4
⇒∠RDQ=∠RAQ
=∠RPQ (proved above)
Hence R,D,P and Q are concyclic.
(∵∠D and ∠P are subtended by RQ on the same side of it.)
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
P, Q and R are, respectively, the mid points of sides BC, CA and AB of a triangle ABC and AD is the perpendicular from vertex A to BC,then prove that the points P,Q,R and D are cyclic.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View Solution
Knowledge Check
If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Aa2+b2+c2=4b2Ba2+b2−c2=4b2Ca2−b2+c2=4b2Da2−b2−c2=4b2If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Ab2=a2−c2Ba2+b2=5c2C3b2=a2−c2D3a2=b2−3c2In a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
If D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
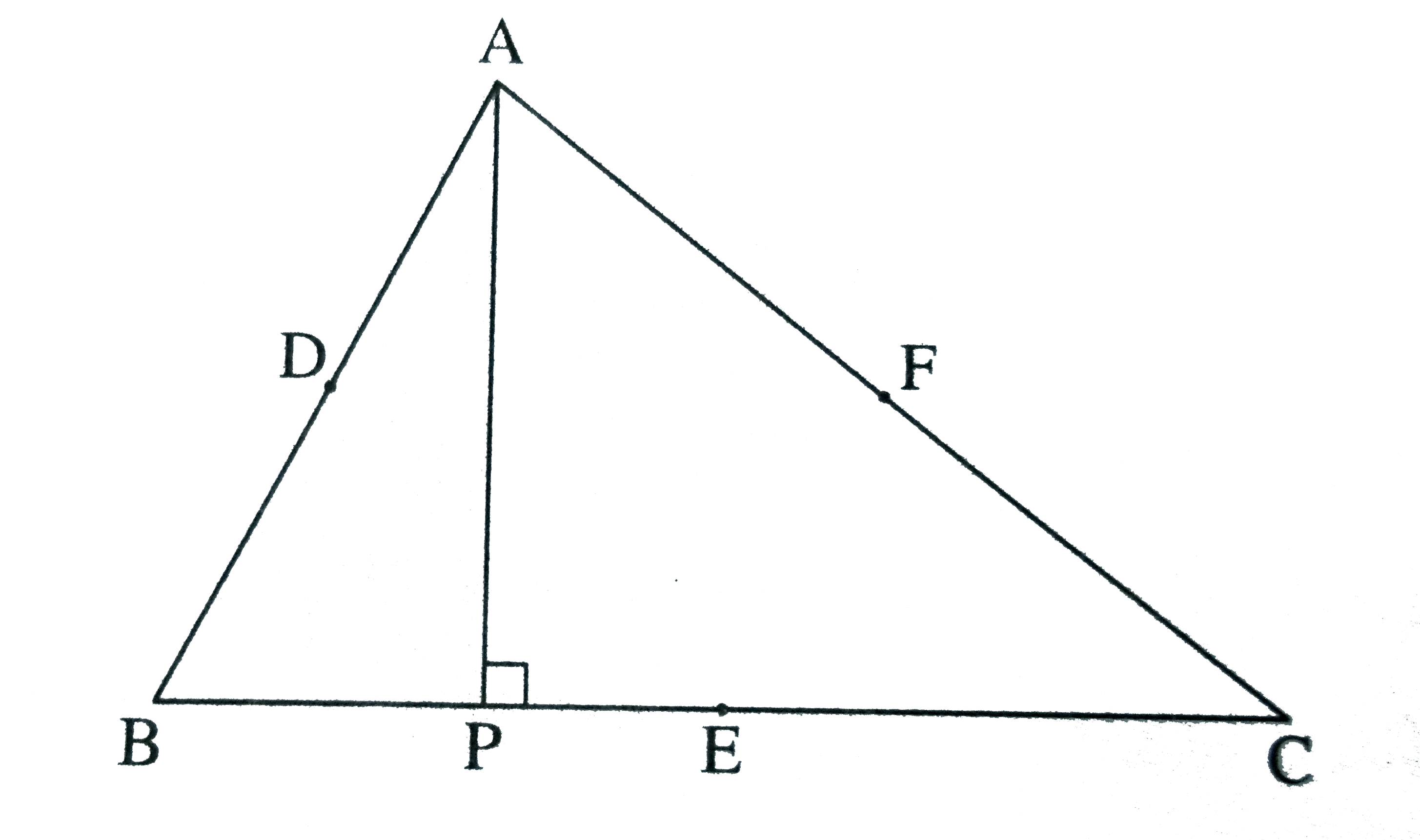
View SolutionIn the figure, D E and F are midpoints of sedes AB,BC and AC respectively. P is the foot of the perpendicular from A to side BC. Show that points D, E,F and P are concyclic.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q are the mid-points of the non-parallel sides BC and AD of a trapezium ABCD·Show that ΔAPD=ΔCQB
View SolutionP and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
View Solution
