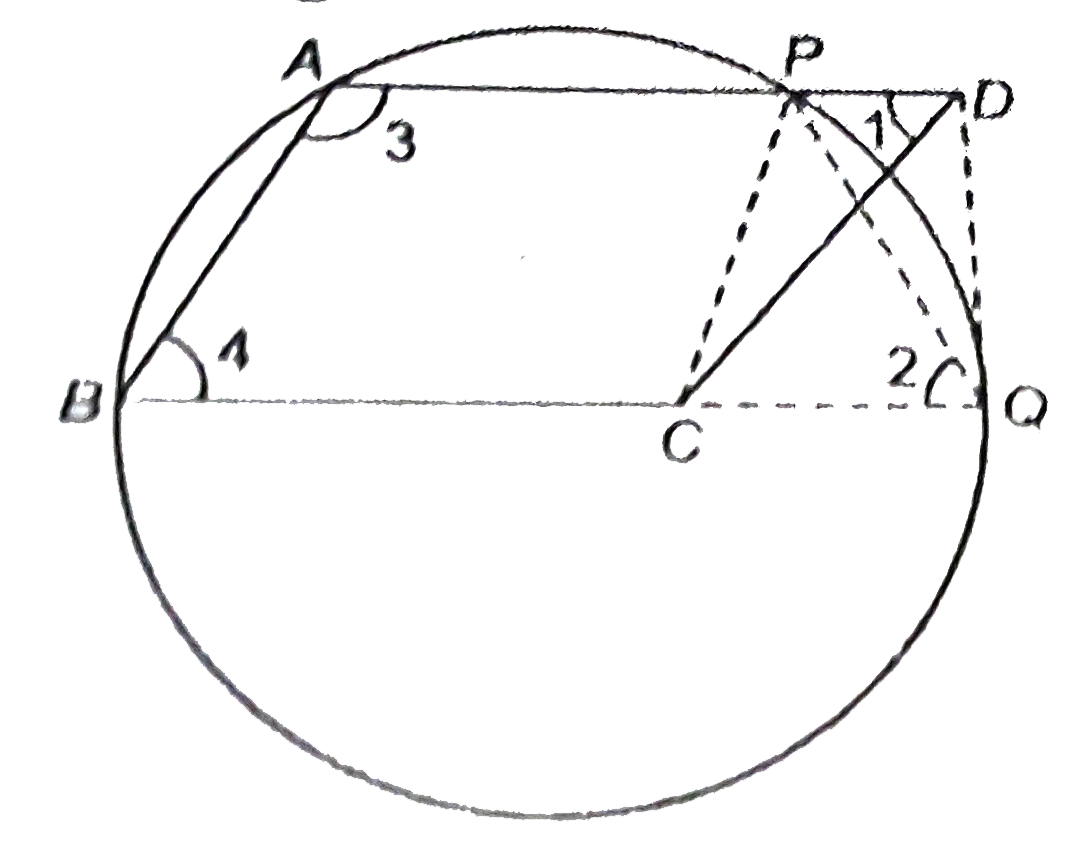
A circle intersects the side AD of a parallelogram ABCD at P and BC produced at Q. Prove that square PDQC is cyclic .
∵AB| |DC
∴∠1+∠3=180∘ (sum of co-interior angles is 180∘) ....(1)
and ∠3+∠2=180∘
(sum of opposite angles of a cyclic quadrilateral )....(2)
∴ From eqs. (1) and (2) , we get
∠1+∠3=∠3+∠2
⇒∠1=∠2
But these are the angles subtended by line segment joining two points P and C lying on the same side of PC.
So, square PDQC is cyclic.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD)
E si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.Show that ΔABE~ΔCFB.
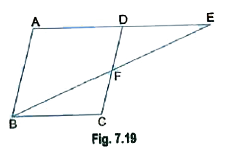
View SolutionABCD is a parallelogram; any line through A cuts DC at a point P and BC produced at Q. prove that triangle BCP is equal in area to triangle DPQ.
View Solution
