AP is tangent to circle O at point P, What is the length of OP?

Video Solution

Text Solution

Verified by Experts

Let the radius of given circle is r.
$∴$ $O P = O B = r$
$∴$ $O A = 2 + r,$ $O P = r,$ $A P = 4$
$∴ O P = O B = r$
$∴ O A = 2 + r, O P = r, A P = 4$
$∠ O P A = 90^{\circ}$ (radius through point of contact is perpendicular to the tangent)

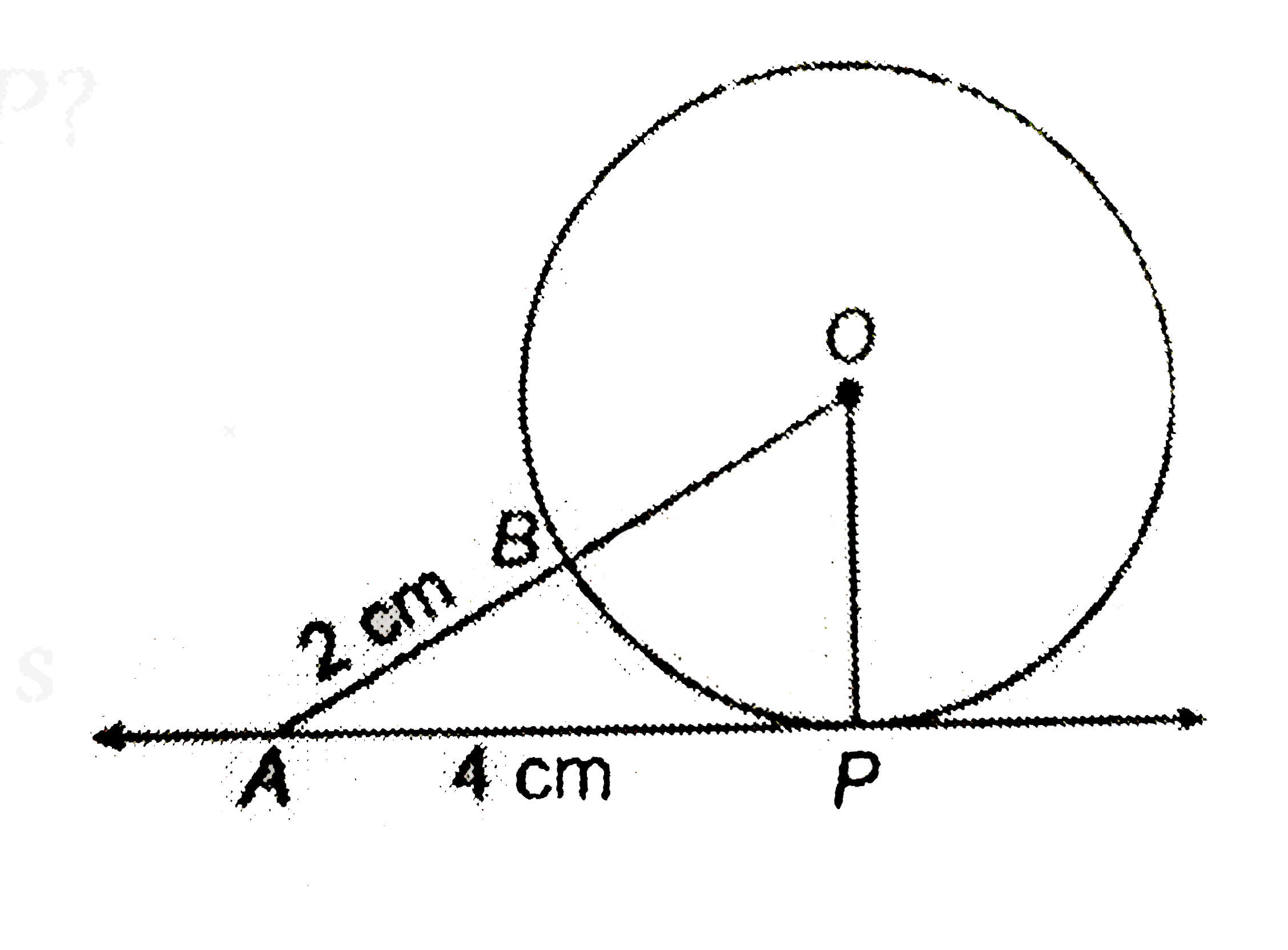
$∴$ In right $△ O P A,$
$O A^{2} = O P^{2} + A P^{2}$ (by Pythagoras theorem)
$(2 + r^{2}) = r^{2} + {(4)}^{2}$
$\Rightarrow 4 + r^{2} + 4 r = r^{2} + 16$
$(2 + r^{2}) = r^{2} + {(4)}^{2}$
$\Rightarrow 4 + r^{2} + 4 r = r^{2} + 16$
$\Rightarrow 4 r = 12 \Rightarrow r = 3$
$∴ O P = 3 c m .$

Updated on:21/07/2023

A circle with radius $r$ has a chord PQ whose length is $2 a$ . The tangents drawn at points $P and Q$ to the circle meet at $T$ , what is the length of $T P$ ?
A $\frac{a r}{\sqrt{r^{2} - a^{2}}}$
B $\frac{2 a r}{\sqrt{r^{2} - a^{2}}}$
C $\frac{r^{2} + a^{2}}{\sqrt{r^{2} - a^{2}}}$
D $\frac{a r}{r - a}$
2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is $120^{\circ}$ ?
A24 cm.
B6 cm.
C8 cm.
DCannot be determined
AP is tangent to the circle with centre O at point A. OP =10 cm and $∠ O P A = 30^{\circ}$ . The radiu of the circle is
A10 cm
B $5 \sqrt{3}$ cm
C5 cm
D $10 \sqrt{3} c m$