A particle is projected at angle θ from horizontal. The product of the two possible times it take to pass over the height h(h<Hmax) is
2ug
2hg
2usinθg
None
The correct Answer is:B
(H−h)=12gt2
t1=√2(H−h)g
t2=√2Hg
T1T2=(√2Hg−√2(H−h)g)(√2Hg+√2(H−h)g)
=2hg
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.

View SolutionA particle is projected so as to have a range R on a horizontal plane through the point of projection and the greatest height attained by it is h. The maximum horizontal range with this velocity of projection is
2h+R28h or u={2g(h+R216h)}1/2
View Solution
Knowledge Check
A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A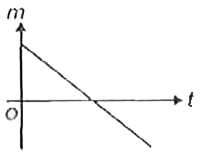 B
B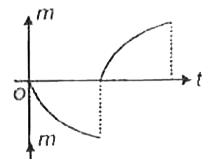 C
C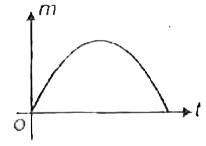 D
D
A particle is projected at an angle with horizontal. If T is the time of flight and R is a horizontal range, then θ is
Acot−1(gT2R)Bcot−1(gT22R)Ctan−1(2RgT2)Dtan−1(gT22R)A particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.A2u2(1+cos2θ)3/2g2√2cosθBu2(1+cos2θ)3/2g2√2cosθCu2(1−sin2θ)3/2g2√2cosθDu2(1−tan2θ)3/2g2√2cosθ
A particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal height h is.
View SolutionA particle is projected from ground at some angle with the horizontal. Let P be the point at maximum height H. At what height above the point P should the particle be aimed to have equal to maximum height ?
View SolutionA particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal height h is.
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionAssertion If a particle is projected vertically upwards with velocity u, the maximum height attained by the particle is h1. The same particle is projected at angle 30∘ from horizontal with the same speed u. Now the maximum height is h2. Thus h1=4h2.
Reason In first case, v=0 at highest point and in second case v≠0 at highest point.
View Solution
