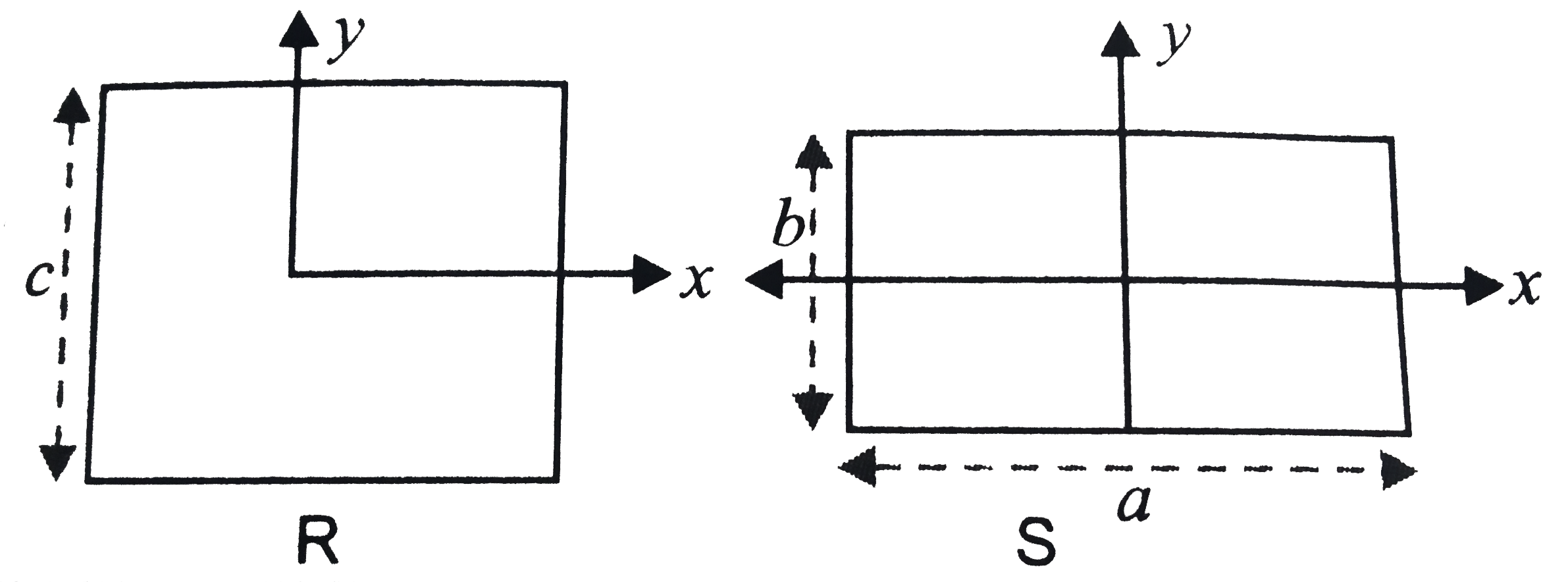
A uniform square plate S(sc) and a unifrom rectangular plate R(sb,a) have identical areas and mass [Fig.]
Show that
(i) IxR/IxS<1, (ii) IyR/IyS>1, (iii) IzR/IzS>1.
![A uniform square plate S (side c) and a unifrom rectangular plate R(side b,a) have identical areas and mass [Fig.] Show that (i) I(xR)//I(xS) lt 1, (ii) I(yR)//I(yS) gt 1, (iii) I(zR)//I(zS) gt 1.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C05_S01_312_Q01.png)
By given question
Area of Squre =Area of rectangular plate
⇒C2=a×b⇒c2=ab
Now by defination
(a)IxRIxs=b2c2 [∵I∝(area)2]
from the diagram Bltc
⇒IxRIxS=(b2c2)<1⇒IxR<Ixs
(b) IyRIys=a2b2
as a gtc
(IyRIys=(ac)2>1
(c ) IzR−Izs∝(a2+b2−2c2)=a2+b2−2ab=(a−b)2 [∵C2=ab]
⇒(IzR−IzS)>0⇒IzRIzs>1
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
A unifrom square plate S(sc) and a unifrom rectangular plate R(sb,a) have identical areas and mass [Fig.]
Show that
(i) IxR/IxS<1, (ii) IyR/IyS>1, (iii) IzR/IzS>1.
View SolutionA uniform square plate S(sc) and a unifrom rectangular plate R(sb,a) have identical areas and mass [Fig.]
Show that
(i) IxR/IxS<1, (ii) IyR/IyS>1, (iii) IzR/IzS>1.

View Solution
Knowledge Check
The moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is
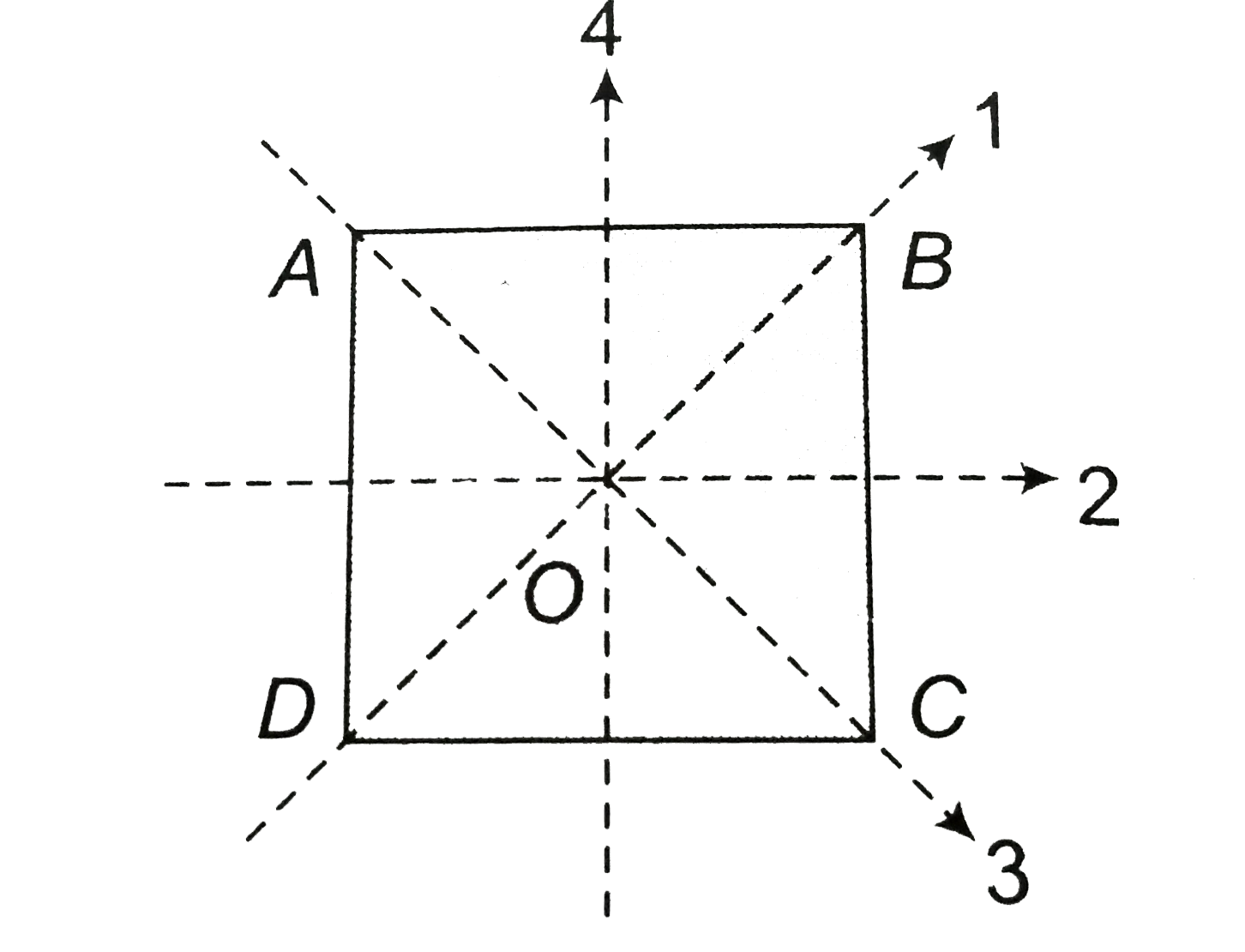
(i) I1+I2
(ii) I2+I4
(iii) I1+I3
(iv) I1+I2+I3+I4
where I1, I2, I3 and I4 are repectively moments of inertia about axes 1, 2, 3 and 4 which are in the plane of the planeA(i),(ii)B(i), (ii), (iii)C(ii), (iii)D(i), (iii)The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
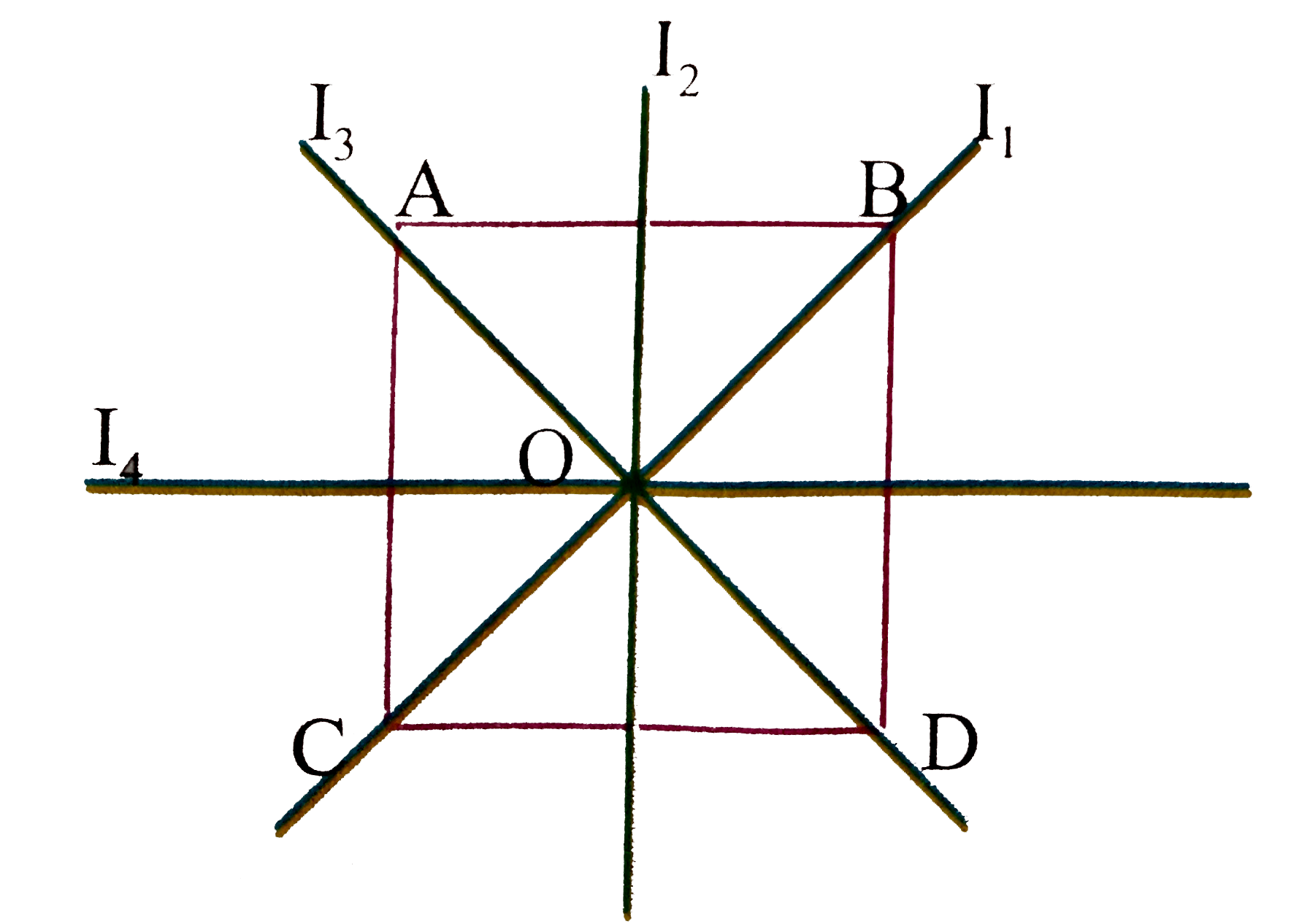
(a)I1+I2, (b)I2+I4
2I1+I3, (d) I1+2I3Aa,b are trueBb,c are trueCc,d are trueDb,d are true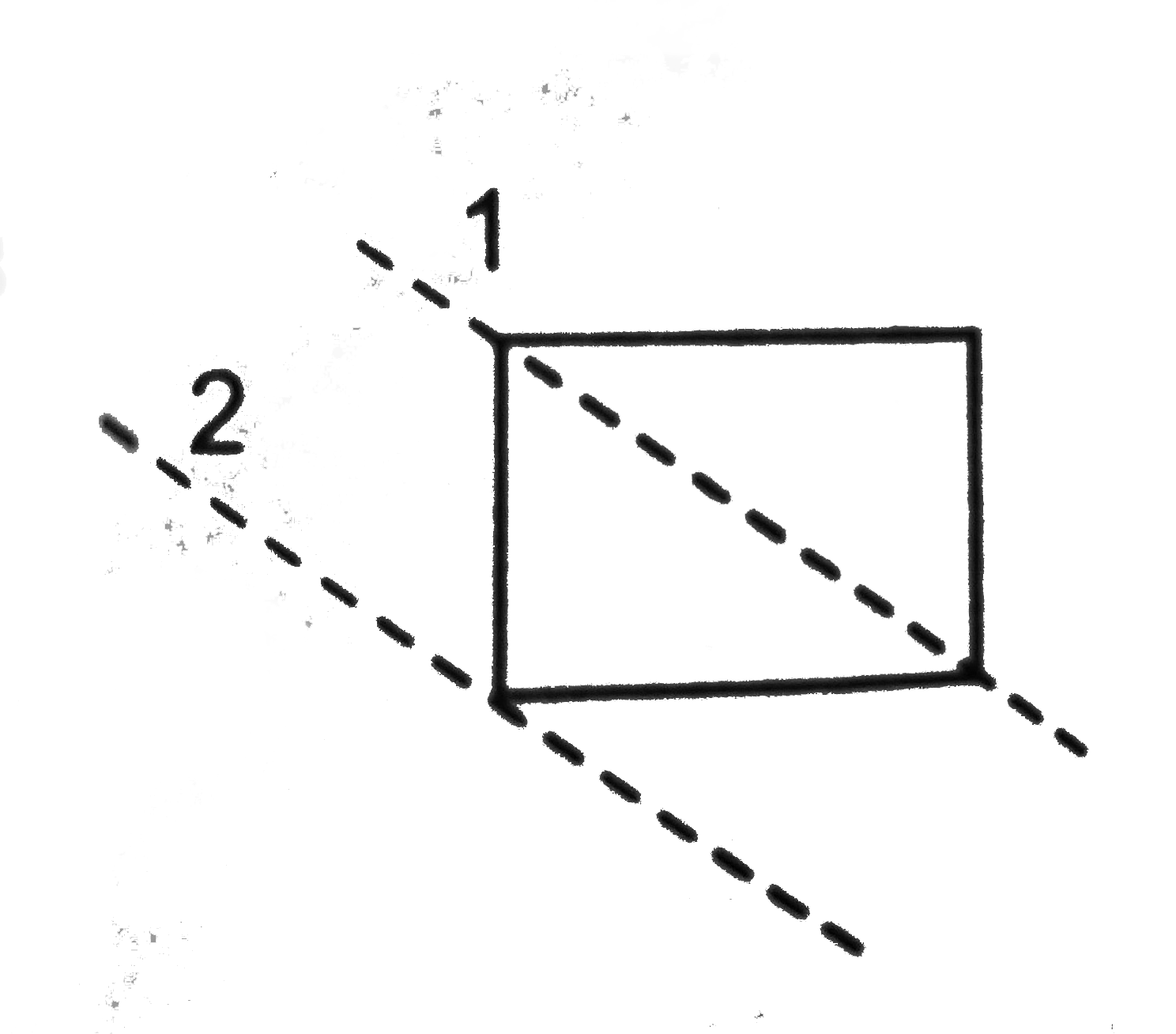
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 isA1:17B1:127C1:712D1:7
Prove that : (i) adj I=I (ii) adj O=O (iii) I−1=I.
View SolutionThe magnitude of gratitational field intensities at distance r1 and r2 from the centre of a uniform solid sphere of radius R and mass M are I1 and I2 respectively. Find the ratio of I1/I2 if (a) r1>R and r2>R and (b) r1<R and r2<R (c ) r1>R and r2<R.
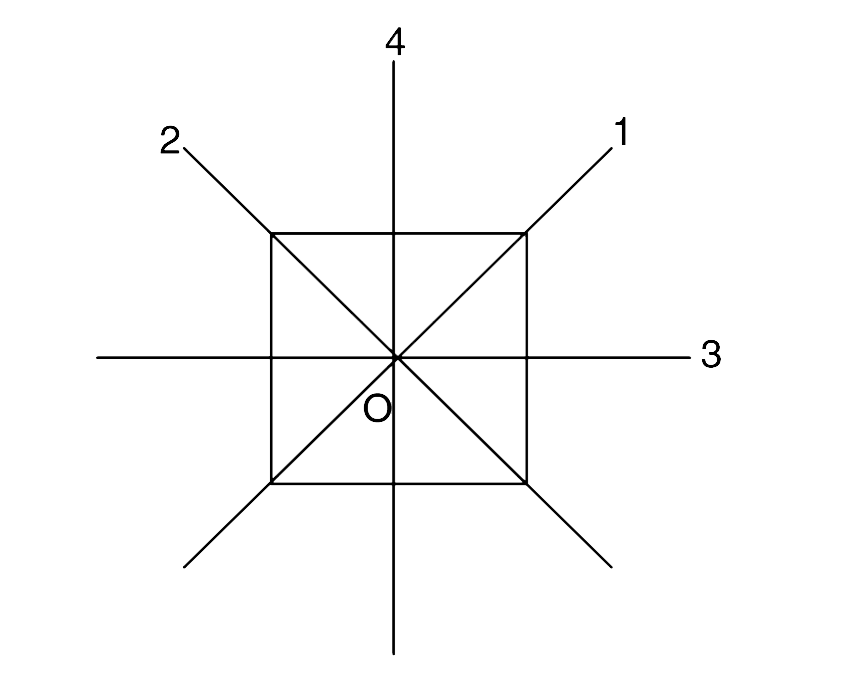
View SolutionConsider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
View SolutionThe ionization potential values of an element are in the following order I1<I2<<<<I3<I4<I5. The element is
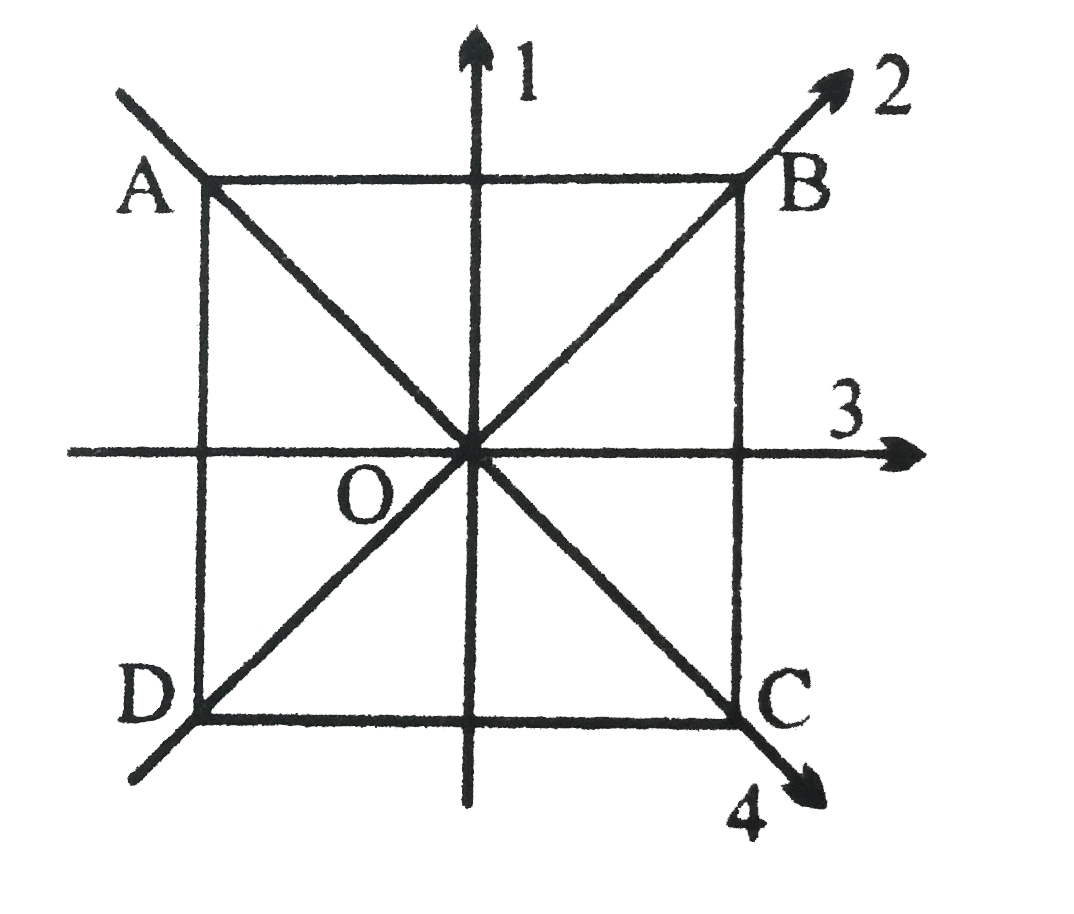
View SolutionABCD is a square plate with centre O. The moments of inertia of the plate about the perpendicular axis through O is I and about the axes 1,2,3,&4 are I1,I2,I3&I4 respectively. It follows that :
 .
.
View Solution
