Two springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
f/2
f/4
4f
2f
The correct Answer is:D
_E01_384_S01.png)
The orginal frequency of osillation
f=12π√k1+k2m
On increasing the k1 and k2 by 4 times, then f
f'=12π√(4k1k2m)=2f
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [B]
Explore 12 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:MCQ s one or more than one correct answers
Explore 5 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [A]
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Two springs of force constants K1 and K2 are connected to a mass m as shown I the figure.

If both K1 and K2 are made four times their original values, the frequency of oscillation becomes,
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
Two springs, of force constants k1 and k2, are connected to a mass maas shown. The frequency of oscillation of mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
 Af/2Bf/4C4fD2f
Af/2Bf/4C4fD2fTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
Two springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
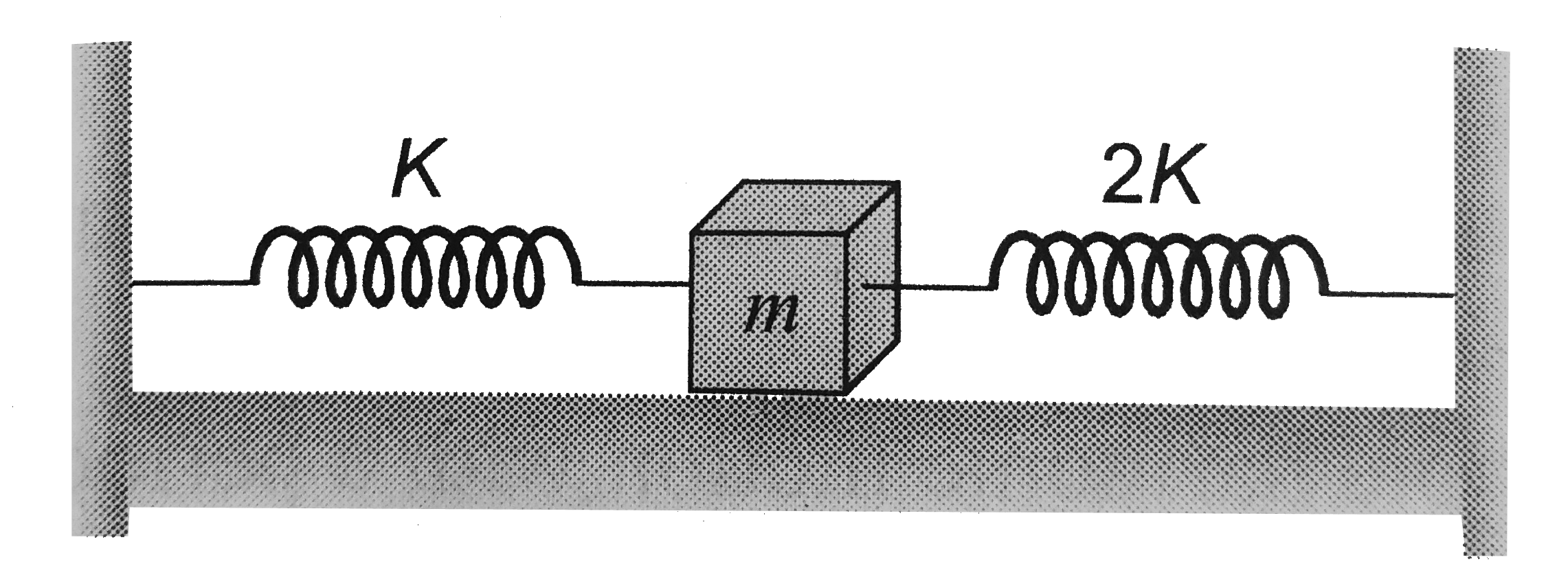
View SolutionInfinite springs with force constants k,2k,4k,8k,….. respectively are connected in series to which mass 'm' is attched. The frequency of small oscillations is……..
View SolutionFour massless springs whose force constants are 2k,2k, k and 2k, respectively, are attached to a mass M kept on a frictionless plane (as shown in figure), If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is

View Solution

