Question

सिद्ध कीजिए कि छोटे द्वारक के अवतल दर्पण की वक्रता त्रिज्या फोकस दुरी से दोगुनी होती है|

Explanation

चित्र में अवतल दर्पण से परावर्तन दर्शाया गया है| RP एक आपतित किरण है जो मुख्य अक्ष के समांतर है एवं अवतल दर्पण से परावर्तन के पश्चात PQ दिशा में गमन करती है एवं मुख्य अक्ष को बिंदु F पर प्रतिच्छेदित करती है| CP रेखा बिंदु P पर अभिलम्ब है| अतः `CP - R` अवतल दर्पण की वक्रता त्रिज्या होगी |
परावर्तन के नियम से
आपतन कोण i = परावर्तन कोण r
या `" "angleRPC=angleQPC`

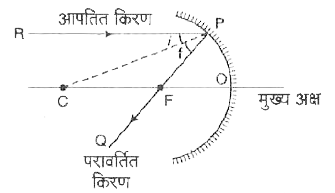
चूँकि आपतित किरण RP मुख्य अक्ष के समान्तर है अतः
`angleRPC= anglePCF` (एकान्तर कोण)
अतः `" "anglePCF=angleQPC=angleFPC`
इसलिए त्रिभुज PCF में
`PF = FC`
यदि दर्पण का द्वारक छोटा हो तो बिंदु P दर्पण के ध्रुव O के समीप होगा |
अतः `" "PF~~OF`
या `" "FC~~OF`
अथवा `" "OF=(1)/(2)OC`
या `" "OC=2OF`
अर्थात जब द्वारक छोटा है तो वक्रता त्रिज्या `OC=R` फोकस दुरी `OF=f` से दोगुनी है एवं फोकस बिंदु F दुरी OC का मध्य बिंदु है |
`R=2f`
अतः स्पष्ट है कि छोटे द्वारक के अवतल दर्पण की वक्रता त्रिज्या फोकस दुरी से दुगुनी होती है|