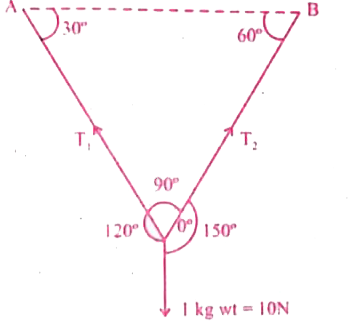
A ball of mass 1 kg hangs in equlibrium from two stings OA and OB in the diagram calcualte the tensions in stings OA and OB take g=10ms−2
 Solution in Tamil
Solution in Tamil
Given mass of the ball
=1kg
g=10ms−1
Various forces acting at the point O are at shown in the diagram .The three forces are in equilibrium .using Lamis theorem
T1sin150∘=T2sin120∘=10sin90∘
and T110sin30∘=10×0.5=5N
and T2=10sin60∘=10×√32
=5√3N
Topper's Solved these Questions
- LAW OF MOTION BOOK - PREMIERS PUBLISHERSCHAPTER - LAW OF MOTION EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (V Conceptual Question )
16 Videos
- KINETIC THEORY OF GASESBOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)
8 Videos
- MOTION OF SYSTEM OF PARTICLES AND BODIESBOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWER (NUMERICAL PROBLEMS)
60 Videos
Similar Questions
Why is it necessary to bend kness while jumping from greater height
View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
View SolutionThe distance between the centres of carbon and oxyen atoms in the carbonmonoxid gas molecule is 1.13Å. Locate the centre of amss of the gas molecule relative to the carbon atom.
View SolutionA ball of mass 1 kg hangs in equilibrium from two string OA and OB as show in figure. What are the tension in string OA and OB ? (Take g= 10 m//s^(2))
View SolutionA ball of mass 1kg hangs in equilibrium from two strings as shown in If g = 10m//s^(2) what are the valuse of tension in strings OA and OB .
View SolutionTwo inclined planes OA and OB of inclinations α and β equal to 30∘ are as shown in the figure. A particle is projected at an angle of 90∘ with plane OA from point A and it strikes the plane OB at point B normally. Then find the speed of projection u in m/s.
(Given that OA=OB=20cm and g=10m/s2)

View Solution(a) A box of weight 10sqrt(3) N is held n equilibrium with the help of two strings OA and OB as shown in figure-1. the string OA is horizontal. Find the tensions in both the stings. (b) If you can change location of the point A on the wall and hence the orientation of the string OA without altering the orientation of the string OB as shown in figure-II. what angle should the string OA make with the wall so that a minimum tension is developed in it?
View Solutionउस सरल रेखा का समीकरण निकालें जो बिंदु (-6, 6) से होकर जाती है तथा अक्षों से क्रमशः ऐसे अंतःखंड OA, OB काटती है ताकि OA -OB = 1.
View Solutionयदि −−→OA=2→i−→j+→k,−−→OB=3→j−5→k तो ∣∣∣−−→OA×−−→OB∣∣∣=
View SolutionA ball of mass 1 kg hangs in equlibrium from two stings OA and OB in the diagram calcualte the tensions in stings OA and OB take g=10ms−2

View SolutionIn the side ABCD rectangle (OA + OB) (OA-OB) = _____ cm
View Solutionवक्तव्य । चित्रानुसार सदिशों OA, OB एवं OC का परिणामी R(1+√2)है। R वृत्त की त्रिज्या है।
वक्तव्य || OA+OC,OB के अनुदिश है तथा (OA+OC)+OB,OB के अनुदिश है।

View SolutionA ball with a mass of 1 kg is hung from the equilibrium of the two cords OA and OB. As shown in the figure, what is the tension in the cords OA and OB? (g = 10 "मी/से"^2 )
View SolutionIf OA and OB circle x^(2) + y^(2) - 2x + 4y = 0 Is the equation of OA and OB, where O is the pivot.
View SolutionA and B are two points on the hyperbola O is the centre. If OA is perpendicular to OB then 1(OA)2+1(OB)2 is equal to
View Solution
