In △ABC,AB=AC and∠B=65∘ then ∠C is equal to
130∘
32∘
70∘
65∘
The correct Answer is:D
To solve the problem step by step, we will use the properties of an isosceles triangle.
Step 1: Identify the triangle type
We are given triangle ABC where AB = AC. This means triangle ABC is an isosceles triangle.
Hint: Remember that in an isosceles triangle, two sides are equal, and the angles opposite those sides are also equal.
Step 2: Use the given angle
We are given that angle B = 65 degrees.
Hint: Keep in mind that the angles in a triangle always sum up to 180 degrees.
Step 3: Set up the equation for the angles
In triangle ABC, since AB = AC, the angles opposite these sides (angle B and angle C) are equal. Therefore, we can say:
- Angle B = Angle C
Since angle B is given as 65 degrees, we can write:
- Angle C = 65 degrees
Hint: Use the property of isosceles triangles that states angles opposite equal sides are equal.
Step 4: Conclusion
Thus, angle C is also 65 degrees.
Final Answer: Angle C = 65 degrees.
We are given triangle ABC where AB = AC. This means triangle ABC is an isosceles triangle.
We are given that angle B = 65 degrees.
In triangle ABC, since AB = AC, the angles opposite these sides (angle B and angle C) are equal. Therefore, we can say:
- Angle B = Angle C
- Angle C = 65 degrees
Thus, angle C is also 65 degrees.
Topper's Solved these Questions
- PRACTICES QUESTION PAPER -3BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICES QUESTION PAPER -3EXERCISE - PART A(Fill in the blank)
1 Videos
- PRACTICES QUESTION PAPER -3BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICES QUESTION PAPER -3EXERCISE - PART B
8 Videos
- PRACTICE TEST QUESTION PAPER 1BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST QUESTION PAPER 1EXERCISE - SECTION-D
5 Videos
- PROBABILITY MIND MAPBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST
6 Videos
Similar Questions
Knowledge Check
If in a triangle ABC as drawn in the figure, AB=AC and ∠ACD=120∘, then ∠A is equal to
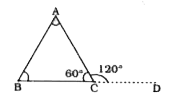 A50∘B60∘C70∘D80∘
A50∘B60∘C70∘D80∘In ΔABC, if AB=AC and ∠B=50∘, then ∠C is equal to
A40∘B50∘C80∘D130∘In △ABC ,AB=AC , ∠B=40∘ Then ∠C is equal to
A50∘B40∘C80∘D140∘
In △ABC,if∠A=65∘ and ∠C=85∘, then ∠B = ?
View SolutionABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
View SolutionIf ΔABC is right - angle at B, AB = 6 units ∠=30∘ then AC is equal to
View SolutionIf a:b=3:2 and b:C=6:5 then a:b:c is equal to
View SolutionIf ΔABC is right - angle at B, AB = 6 units ∠=30∘ then AC is equal to
View Solution
