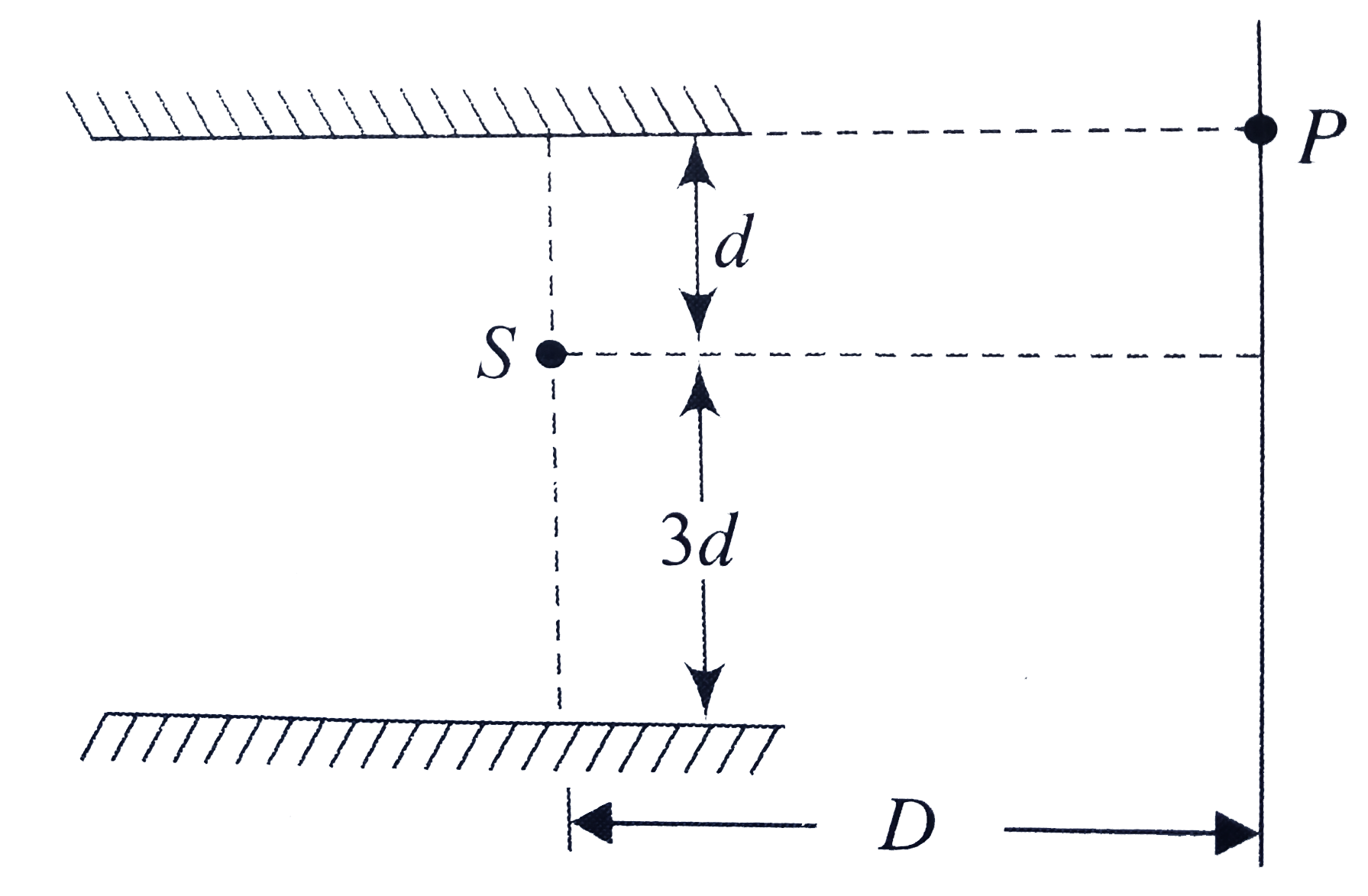
Consider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
12d2D
6d2D
3d2D
24d2D
The correct Answer is:1
At P, Δx=(8d)×3dD. For 2nd maxima, Δx=2λ⇒24d2D=2λ⇒λ=12d2D
Similar Questions
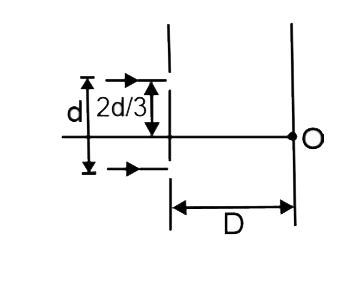
In the figure shown if a parallel beam of white light is incident on the plane of the slits then the distance of the white spot on the screen from O is [Assume <<D,λ<<d]
View SolutionThree narrow slits A, B and C are illuminated by a parallel beam of light of wavelengthλ , P is a point on the screen exactly in front of point A. Slit plane is at a distance D from the screen(D>>λ). It is know that BP – AP =13
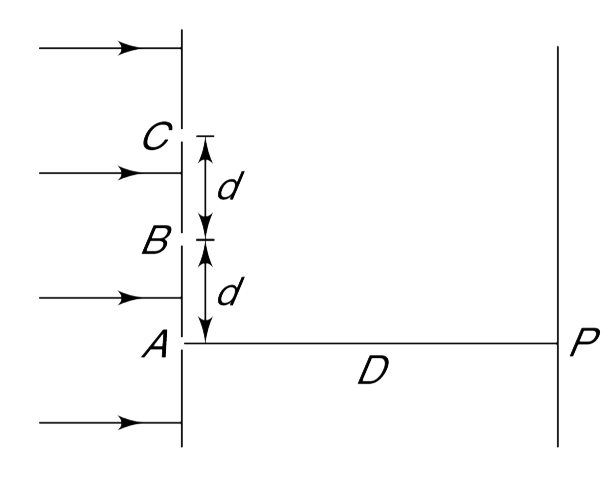
(a) Find d in terms of D andλ
(b) Write the phase difference between waves reaching at P from C and A.
(c) If intensity of P due to any of the three slits individu- ally is I0, find the resultant intensity at P.
View Solution
Knowledge Check
Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
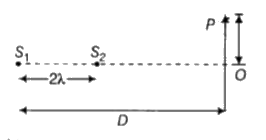 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5DLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is ––
Ad2λB2dλC2d2λDd22λTwo points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
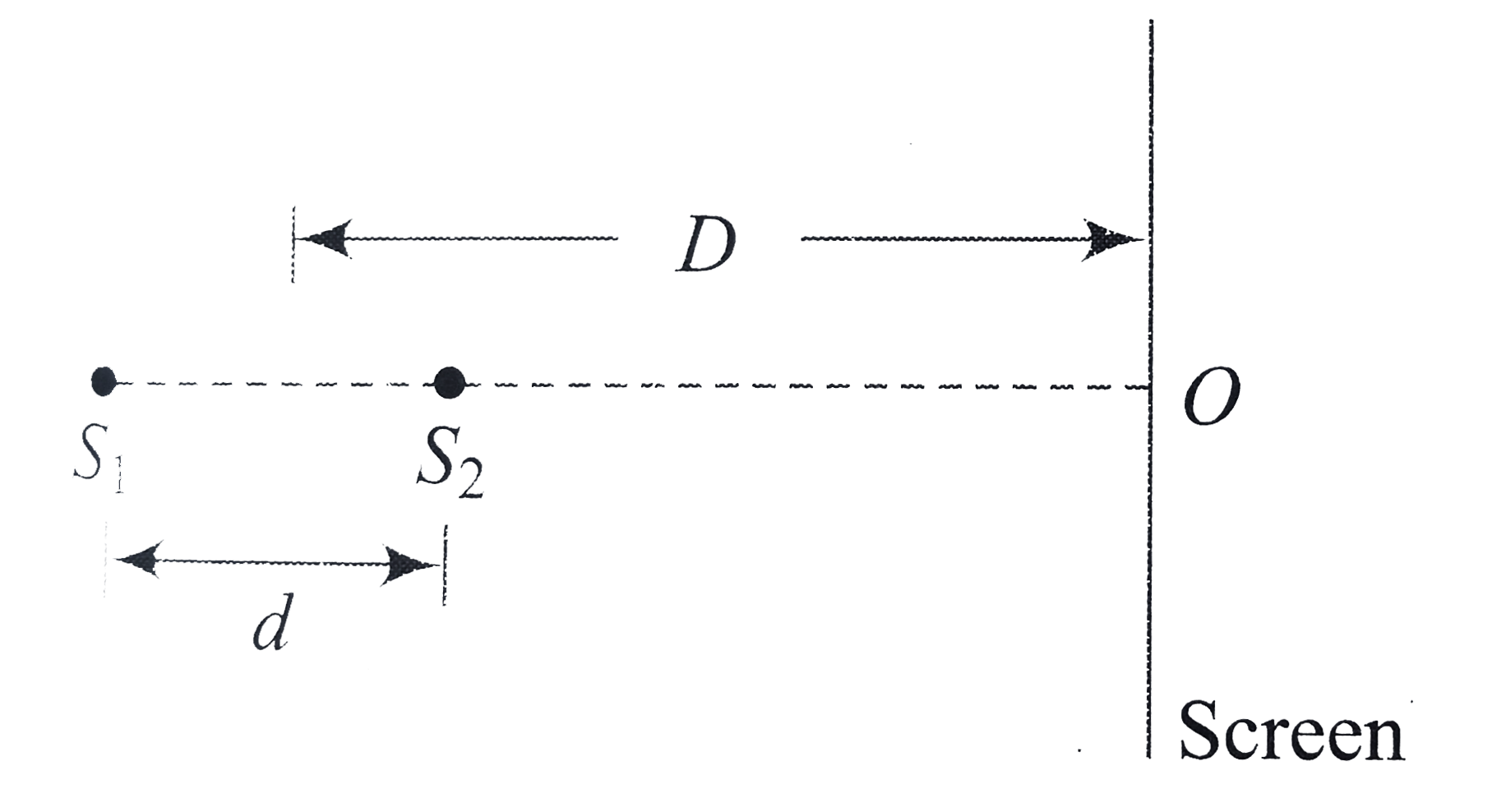 AIf d=7λ2, O will be a minimaBIf d=λ, only one maxima can be observed on the screenCIf d=4.8λ, then total 10 minima would be there on the screenDIf d=5λ2, the intensity at O would be minimum.
AIf d=7λ2, O will be a minimaBIf d=λ, only one maxima can be observed on the screenCIf d=4.8λ, then total 10 minima would be there on the screenDIf d=5λ2, the intensity at O would be minimum.
Three coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

View SolutionIn a Young's double-slit experiment, if the incident light consists of two wavelengths λ1 and λ2, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to each wavelength will coincide at a distance from the central maxima, given by
View SolutionFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

View SolutionLight from two coherent sources of the same amplitude A and wavelength λ illuminates the screen. The intensity of the central maximum is I0. If the sources were incoherent, the intensity at the same point will be
View SolutionA driver is riding a car with velocity vc between two vertical walls on a horizontal surface as shown in figure.A source of sound of frequency 'f' is situated on the car. (vc<<v, where v is the speed of sound in air )

Consider the sound wave observed by the driver directly from car has a wavelength λ1 and the sound wave after reflection from wall-1 observed by the driver has wavelength λ2 then λ1−λ2λ1+λ2 is :
View Solution
